友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
Union Find Set 并查集
并查集算法,英文是 Union-Find,是解决动态连通性(Dynamic Conectivity)问题的一种算法。动态连通性是计算机图论中的一种数据结构,动态维护图结构中相连信息。简单的说就是,图中各个节点之间是否相连、如何将两个节点连接,连接后还剩多少个连通分量。
动态连通性其实可以抽象成给一幅图连线。假设用一个数组表示一堆节点,每个节点都是一个连通分量。初始化视图如下:
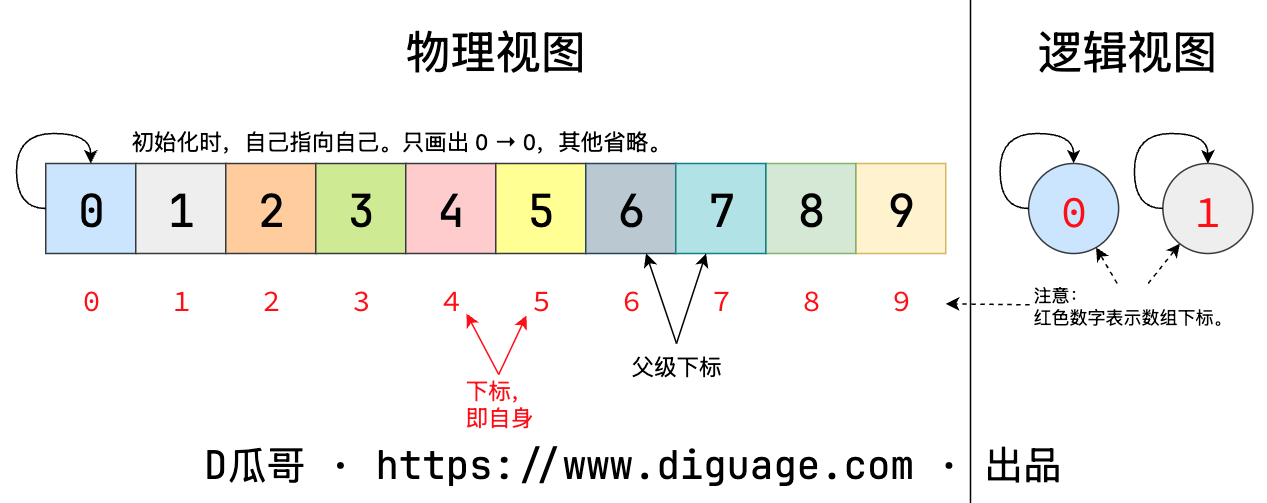
并查集的一个重要操作是 union(a, b),就是将节点 a 和节点 b 建立连接。如图所示:
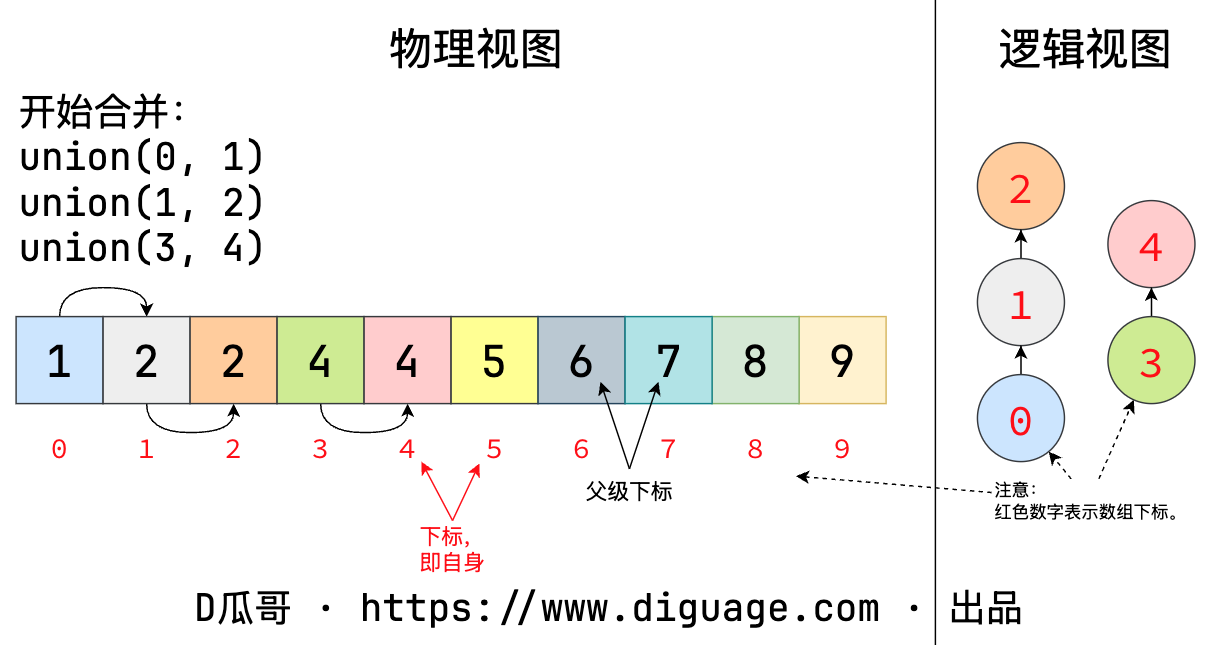
union(a, b) 还可以将已经建立的两个“子网”进行连接:
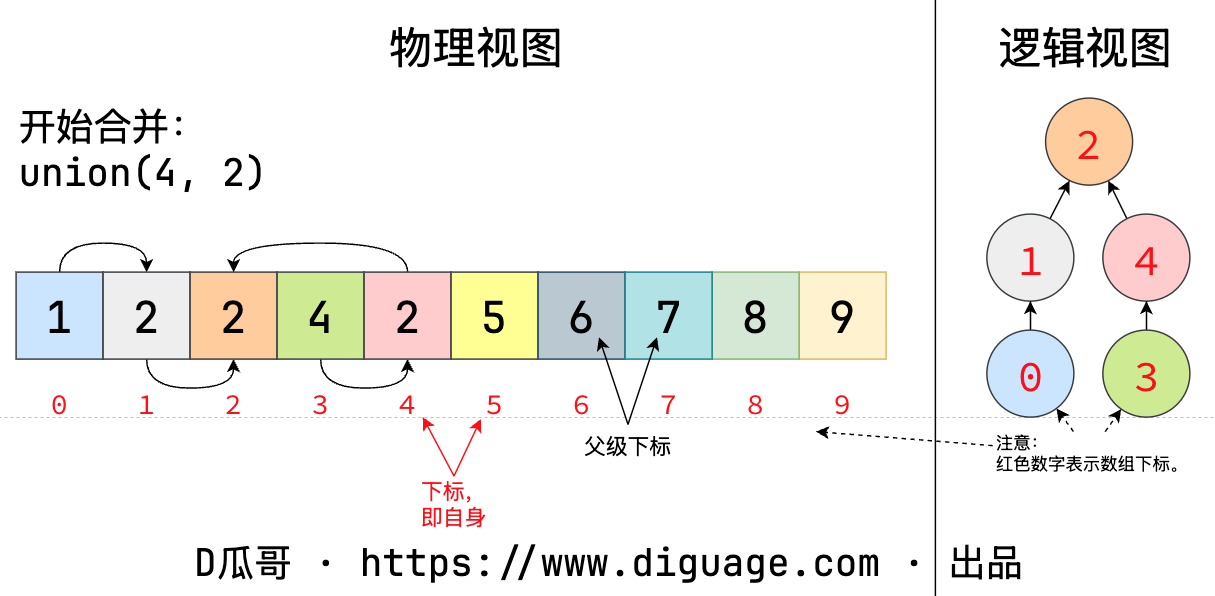
在合并时,是修改根节点的指针 parent[ap] = bp,而不是修改节点的指针 parent[a] = bp。
|
并查集除了 union,还有一个重要操作是 connnected(a, b)。判断方法也很简单,从节点 a 和 b 开始,向上查找,直到两个节点的根节点,判断两个根节点是否相等即可判断两个节点是否已经连接。为了加快这个判断速度,可以对其进行“路径压缩”,直白点说,就是将所有树的节点,都直接指向根节点,这样只需要一步即可到达根节点。路径压缩如图所示:
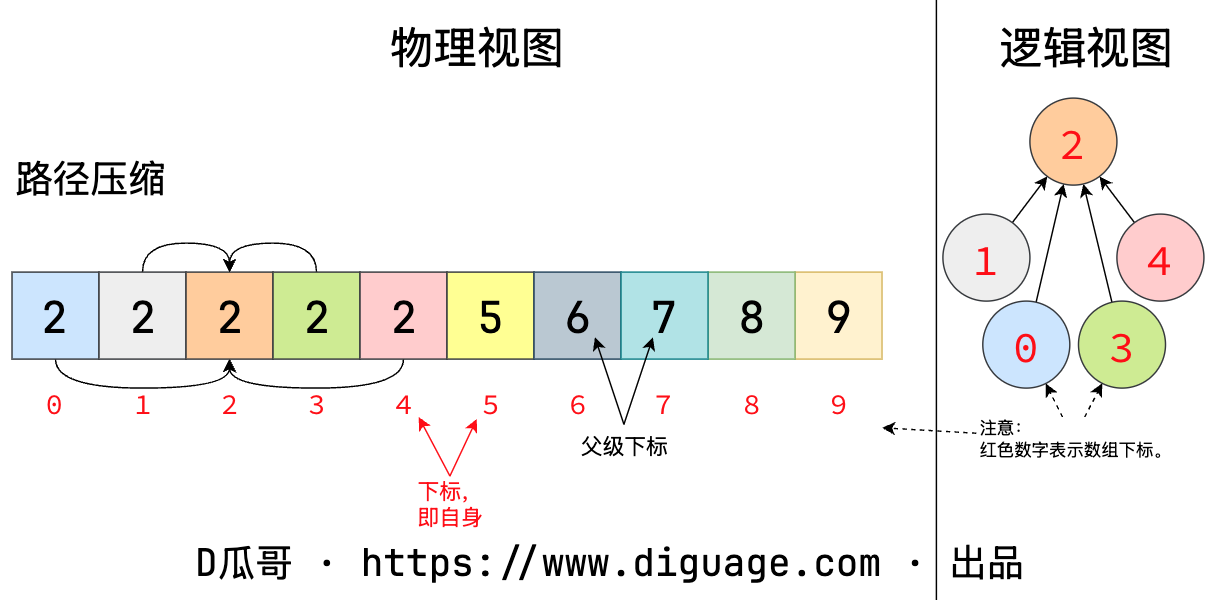
简单代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
package com.diguage.labs;
import java.util.ArrayList;
import java.util.List;
/**
* 并查集
*
* PS:没想到代码竟然一次通过。
*
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-03 15:22:41
*/
public class UnionFind {
/**
* 连通分量
*/
private int size;
/**
* 每个节点及对应的父节点
*/
private int[] parent;
public UnionFind(int size) {
this.size = size;
parent = new int[size];
// 自己指向自己
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
/**
* a 和 b 建立连接
*/
public void union(int a, int b) {
int ap = find(a);
int bp = find(b);
if (ap == bp) {
return;
}
parent[ap] = bp;
size--;
}
/**
* a 和 b 是否连通
*/
public boolean connected(int a, int b) {
int ap = find(a);
int bp = find(b);
return ap == bp;
}
/**
* 连通分量
*/
public int count() {
return size;
}
/**
* 查找节点 a 的根节点
*/
private int find(int a) {
int ap = parent[a];
if (a != ap) {
List<Integer> path = new ArrayList<>();
path.add(a);
// 向上查找根节点
while (parent[ap] != ap) {
path.add(ap);
ap = parent[ap];
}
// 路径压缩
// 只有一步,无需缩短路径
if (path.size() == 1) {
return ap;
}
for (Integer idx : path) {
parent[idx] = ap;
}
}
return ap;
}
public static void main(String[] args) {
UnionFind uf = new UnionFind(10);
uf.union(0, 1);
uf.union(1, 2);
uf.union(2, 3);
uf.union(3, 4);
uf.union(5, 6);
uf.union(6, 7);
uf.union(7, 8);
uf.union(8, 9);
uf.union(0, 5);
System.out.println(uf.count() + ", " + uf.connected(0, 9));
System.out.println(uf.count() + ", " + uf.connected(2, 9));
System.out.println(uf.count() + ", " + uf.connected(3, 9));
System.out.println(uf.count() + ", " + uf.connected(5, 9));
}
}
经典题目
-
[0323-number-of-connected-components-in-an-undirected-graph]
-
[1489-find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree]
-
[1579-remove-max-number-of-edges-to-keep-graph-fully-traversable]
-
[2334-subarray-with-elements-greater-than-varying-threshold]
-
[2948-make-lexicographically-smallest-array-by-swapping-elements]

