友情支持
如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜
|
|
有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。
公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
222. Count Complete Tree Nodes
Given a complete binary tree, count the number of nodes.
*Note: *
Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Example:
Input:
1
/ \
2 3
/ \ /
4 5 6
Output: 6思路分析
官方题解给的方案是：“二分查找 + 位运算”，坦白讲，这个方案有些扯淡。而且不容易理解。
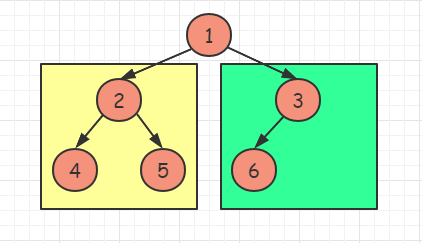
完全二叉树是一棵空树或者它的叶子节点只出在最后两层，若最后一层不满则叶子节点只在最左侧。
满二叉的节点个数计算方法：如果满二叉树的层数为h，则总节点数为：2h - 1.
对 root 节点的左右子树进行高度统计，分别记为 left 和 right，有以下两种结果：
-
left == right。这说明，左子树一定是满二叉树，因为节点已经填充到右子树了，左子树必定已经填满了。所以左子树的节点总数我们可以直接得到，是 2left - 1，加上当前这个root节点，则正好是 2left。再对右子树进行递归统计。
-
left != right。说明此时最后一层不满，但倒数第二层已经满了，可以直接得到右子树的节点个数。同理，右子树节点 +root节点，总数为 2right。再对左子树进行递归查找。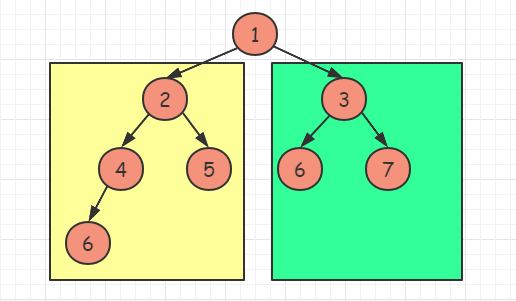
根据下面这张图：
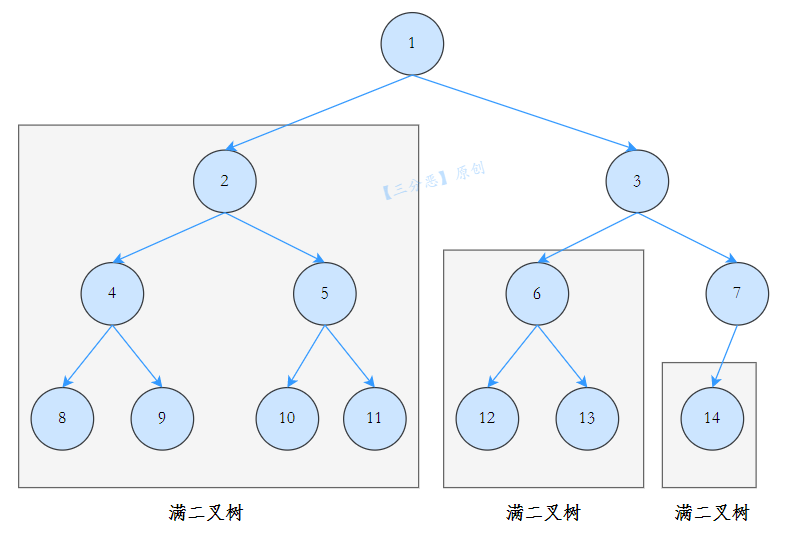
再结合代码，就更容易理解了。
如何计算 2left，最快的方法是移位计算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
// countLevel 方法统计的是最节点的深度
int left = countLevel(root.left);
int right = countLevel(root.right);
if (left == right) {
return countNodes(root.right) + (1 << left);
} else {
return countNodes(root.left) + (1 << right);
}
}
private int countLevel(TreeNode root) {
int result = 0;
while (root != null) {
// 注意：这里是 left 节点
root = root.left;
result++;
}
return result;
}