友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
480. 滑动窗口中位数
中位数是有序序列最中间的那个数。如果序列的长度是偶数,则没有最中间的数;此时中位数是最中间的两个数的平均数。
例如:
-
[2,3,4],中位数是3 -
[2,3],中位数是(2 + 3) / 2 = 2.5
给你一个数组 nums,有一个长度为 k 的窗口从最左端滑动到最右端。窗口中有 k 个数,每次窗口向右移动 1 位。你的任务是找出每次窗口移动后得到的新窗口中元素的中位数,并输出由它们组成的数组。
示例:
给出 nums = [1,3,-1,-3,5,3,6,7],以及 k = 3。
窗口位置 中位数 --------------- ----- [1 3 -1] -3 5 3 6 7 1 1 [3 -1 -3] 5 3 6 7 -1 1 3 [-1 -3 5] 3 6 7 -1 1 3 -1 [-3 5 3] 6 7 3 1 3 -1 -3 [5 3 6] 7 5 1 3 -1 -3 5 [3 6 7] 6
因此,返回该滑动窗口的中位数数组 `[1,-1,-1,3,5,6]`。
提示:
-
你可以假设
k始终有效,即:k始终小于等于输入的非空数组的元素个数。 -
与真实值误差在
10-5以内的答案将被视作正确答案。
思路分析
利用 295. 数据流的中位数 中的 Two Heaps 对顶堆 在“运动”中,删除,添加,求中位数。
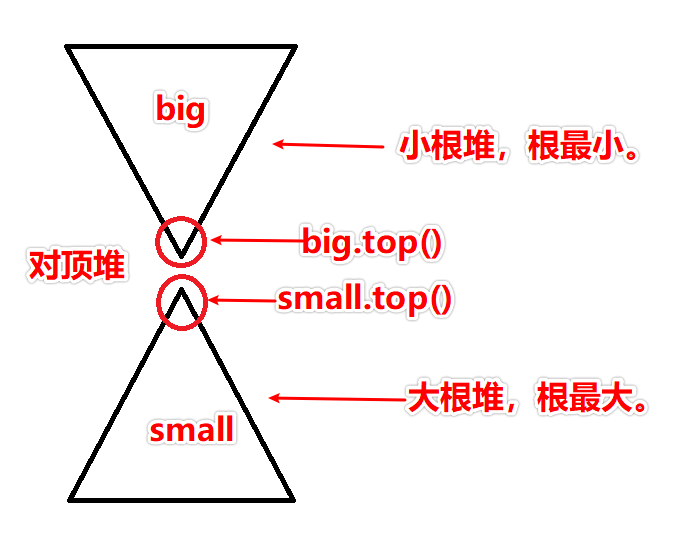
直接使用对顶堆会超时!加上延迟删除技巧,就可以通过。所谓延迟删除技巧,就是只删除堆顶,其余只做删除标记。这样,就不用耗时去堆里遍历查找要删除的元素。
-
一刷(超时)
-
二刷(超时)
-
三刷
-
四刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
* 答案是正确的,超大数组测试时,超时了。
*
* @author D瓜哥 · https://www.diguage.com
* @since 2024-08-30 11:45:50
*/
public double[] medianSlidingWindow(int[] nums, int k) {
// 如果窗口是奇数,则 topSmall 多一个
Queue<Integer> topSmall = new PriorityQueue<>((a, b) -> Integer.compare(a, b));
// 使用 Integer.compare,防止两个最小负数相减时溢出
Queue<Integer> topLarge = new PriorityQueue<>((a, b) -> Integer.compare(b, a));
double[] result = new double[nums.length - k + 1];
for (int i = 0; i < k; i++) {
topSmall.add(nums[i]);
}
for (int i = 0; i < k / 2; i++) {
topLarge.add(topSmall.poll());
}
// 先相处再相加,防止溢出
result[0] = k % 2 == 1 ? 1.0 * topSmall.peek()
: topSmall.peek() / 2.0 + topLarge.peek() / 2.0;
for (int i = k; i < nums.length; i++) {
int num = nums[i];
if (topSmall.peek() <= num) {
topSmall.add(num);
} else {
topLarge.add(num);
}
int delNum = nums[i - k];
if (topSmall.peek() <= delNum) {
topSmall.remove(delNum);
} else {
topLarge.remove(delNum);
}
// 添加,删除,再平衡双堆,这样才能保证堆的平衡性
// topSmall 应该始终大于等于 topLarge
while (topLarge.size() > topSmall.size()) {
topSmall.add(topLarge.poll());
}
// topSmall 与 topLarge 的差值不能大于 1
while (topSmall.size() - topLarge.size() > 1) {
topLarge.add(topSmall.poll());
}
result[i - k + 1] = k % 2 == 1 ? 1.0 * topSmall.peek()
: topSmall.peek() / 2.0 + topLarge.peek() / 2.0;
}
return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
* 优化前,通过 43 / 44 个测试用例。
*
* @author D瓜哥 · https://www.diguage.com
* @since 2025-09-15 22:04:02
*/
public double[] medianSlidingWindow(int[] nums, int k) {
PriorityQueue<Integer> topSmall = new PriorityQueue<>();
PriorityQueue<Integer> topLarge = new PriorityQueue<>((a, b) -> Integer.compare(b, a));
double[] result = new double[nums.length - k + 1];
int index = 0;
while (index < nums.length) {
int num = nums[index];
if (topLarge.isEmpty() || topLarge.peek() >= num) {
topLarge.add(num);
} else {
topSmall.add(num);
}
if (k <= index) {
int delete = nums[index - k];
if (delete > topLarge.peek()) {
topSmall.remove(delete);
} else {
topLarge.remove(delete);
}
}
while (topSmall.size() > topLarge.size()) {
topLarge.offer(topSmall.poll());
}
while (topLarge.size() - topSmall.size() > 1) {
topSmall.offer(topLarge.poll());
}
if (topSmall.size() + topLarge.size() == k) {
result[index - k + 1] = getMedian(k, topSmall, topLarge);
}
index++;
}
return result;
}
private static double getMedian(int k, PriorityQueue<Integer> topSmall, PriorityQueue<Integer> topLarge) {
if ((k & 1) == 1) {
return topLarge.peek();
}
return (0D + topSmall.peek() + topLarge.peek()) / 2.0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-10-16 22:41:00
*/
public double[] medianSlidingWindow(int[] nums, int k) {
List<Double> result = new ArrayList<>();
MedianFinder finder = new MedianFinder();
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
finder.addNum(num);
if (finder.size() < k) {
continue;
}
result.add(finder.findMedian());
int deleted = nums[i - k + 1];
finder.deleteNum(deleted);
}
return result.stream().mapToDouble(i -> i).toArray();
}
private static class MedianFinder {
private final PriorityQueue<Integer> topSmallHeap;
private final PriorityQueue<Integer> topLargeHeap;
private int topSmallSize;
private int topLargeSize;
private Map<Integer, Integer> waitDelateNum;
public MedianFinder() {
topSmallHeap = new PriorityQueue<>();
topSmallSize = 0;
topLargeHeap = new PriorityQueue<>((a, b) -> Integer.compare(b, a));
topLargeSize = 0;
waitDelateNum = new HashMap<>();
}
public void addNum(int num) {
if (Objects.equals(topSmallSize, topLargeSize)) {
deleteTop(topLargeHeap);
topLargeHeap.offer(num);
topSmallHeap.offer(topLargeHeap.poll());
topSmallSize++;
} else {
deleteTop(topSmallHeap);
topSmallHeap.offer(num);
topLargeHeap.offer(topSmallHeap.poll());
topLargeSize++;
}
}
public void deleteNum(int num) {
if (!topLargeHeap.isEmpty() && num <= topLargeHeap.peek()) {
waitDelateNum.put(num, waitDelateNum.getOrDefault(num, 0) + 1);
deleteTop(topLargeHeap);
topLargeSize--;
} else if (!topSmallHeap.isEmpty() && num >= topSmallHeap.peek()) {
waitDelateNum.put(num, waitDelateNum.getOrDefault(num, 0) + 1);
deleteTop(topSmallHeap);
topSmallSize--;
}
if (topLargeSize > topSmallSize) {
deleteTop(topLargeHeap);
topSmallHeap.offer(topLargeHeap.poll());
topLargeSize--;
topSmallSize++;
}
if (topSmallSize - topLargeSize > 1) {
deleteTop(topSmallHeap);
topLargeHeap.offer(topSmallHeap.poll());
topSmallSize--;
topLargeSize++;
}
}
public double findMedian() {
if (Objects.equals(topSmallSize, topLargeSize)) {
deleteTop(topSmallHeap);
deleteTop(topLargeHeap);
return (0.0D + topLargeHeap.peek() + topSmallHeap.peek()) / 2.0;
} else {
deleteTop(topSmallHeap);
return topSmallHeap.peek();
}
}
public int size() {
return topSmallHeap.size() + topLargeHeap.size();
}
private void deleteTop(PriorityQueue<Integer> queue) {
while (!queue.isEmpty() && waitDelateNum.getOrDefault(queue.peek(), 0) > 0) {
int deleted = queue.poll();
waitDelateNum.put(deleted, waitDelateNum.get(deleted) - 1);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-12-13 22:22:04
*/
public double[] medianSlidingWindow(int[] nums, int k) {
List<Double> result = new ArrayList<>();
MedianFinder finder = new MedianFinder();
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
finder.addNum(num);
if (finder.size() < k) {
continue;
}
result.add(finder.findMedian());
int deleted = nums[i - k + 1];
finder.deleteNum(deleted);
}
return result.stream().mapToDouble(i -> i).toArray();
}
private static class MedianFinder {
private final PriorityQueue<Integer> topSmallHeap;
private final PriorityQueue<Integer> topLargeHeap;
private int topSmallSize;
private int topLargeSize;
private Map<Integer, Integer> waitDelateNum;
public MedianFinder() {
topSmallHeap = new PriorityQueue<>();
topSmallSize = 0;
topLargeHeap = new PriorityQueue<>((a, b) -> Integer.compare(b, a));
topLargeSize = 0;
waitDelateNum = new HashMap<>();
}
public void addNum(int num) {
if (Objects.equals(topSmallSize, topLargeSize)) {
deleteTop(topLargeHeap);
topLargeHeap.offer(num);
topSmallHeap.offer(topLargeHeap.poll());
topSmallSize++;
} else {
deleteTop(topSmallHeap);
topSmallHeap.offer(num);
topLargeHeap.offer(topSmallHeap.poll());
topLargeSize++;
}
}
public void deleteNum(int num) {
if (!topLargeHeap.isEmpty() && num <= topLargeHeap.peek()) {
waitDelateNum.put(num, waitDelateNum.getOrDefault(num, 0) + 1);
deleteTop(topLargeHeap);
topLargeSize--;
} else if (!topSmallHeap.isEmpty() && num >= topSmallHeap.peek()) {
waitDelateNum.put(num, waitDelateNum.getOrDefault(num, 0) + 1);
deleteTop(topSmallHeap);
topSmallSize--;
}
if (topLargeSize > topSmallSize) {
deleteTop(topLargeHeap);
topSmallHeap.offer(topLargeHeap.poll());
topLargeSize--;
topSmallSize++;
}
if (topSmallSize - topLargeSize > 1) {
deleteTop(topSmallHeap);
topLargeHeap.offer(topSmallHeap.poll());
topSmallSize--;
topLargeSize++;
}
}
public double findMedian() {
if (Objects.equals(topSmallSize, topLargeSize)) {
deleteTop(topSmallHeap);
deleteTop(topLargeHeap);
return (0.0D + topLargeHeap.peek() + topSmallHeap.peek()) / 2.0;
} else {
deleteTop(topSmallHeap);
return topSmallHeap.peek();
}
}
public int size() {
return topSmallHeap.size() + topLargeHeap.size();
}
private void deleteTop(PriorityQueue<Integer> queue) {
while (!queue.isEmpty() && waitDelateNum.getOrDefault(queue.peek(), 0) > 0) {
int deleted = queue.poll();
waitDelateNum.put(deleted, waitDelateNum.get(deleted) - 1);
}
}
}
// private static class DualHeap {
// private Map<Integer, Integer> counter;
// private PriorityQueue<Integer> topSmallHeap;
// private PriorityQueue<Integer> topLargeHeap;
// private int topSmallHeapSize;
// private int topLargeHeapSize;
//
// public DualHeap(int capacity) {
// counter = new HashMap<>();
// topSmallHeap = new PriorityQueue<>();
// topSmallHeapSize = 0;
// topLargeHeap = new PriorityQueue<>((a, b) -> b - a);
// topLargeHeapSize = 0;
// }
//
// public void offer(int num) {
// if (Objects.equals(topSmallHeapSize, topLargeHeapSize)) {
// topLargeHeap.offer(num);
// pollRemovedTop(topLargeHeap);
// Integer top = topLargeHeap.poll();
// topSmallHeap.offer(top);
// topSmallHeapSize++;
// } else {
// topSmallHeap.offer(num);
// pollRemovedTop(topSmallHeap);
// Integer top = topSmallHeap.poll();
// topLargeHeap.offer(top);
// topLargeHeapSize++;
// }
// }
//
// public void deleteNum(int num) {
// if (!topLargeHeap.isEmpty() && num <= topLargeHeap.peek()) {
// counter.put(num, counter.getOrDefault(num, 0) + 1);
// pollRemovedTop(topLargeHeap);
// topLargeHeapSize--;
// } else if (!topSmallHeap.isEmpty() && num >= topSmallHeap.peek()) {
// counter.put(num, counter.getOrDefault(num, 0) + 1);
// pollRemovedTop(topSmallHeap);
// topSmallHeapSize--;
// }
//
// if (topLargeHeapSize > topSmallHeapSize) {
// pollRemovedTop(topLargeHeap);
// topSmallHeap.offer(topLargeHeap.poll());
// topLargeHeapSize--;
// topSmallHeapSize++;
// }
// if (topSmallHeapSize - topLargeHeapSize > 1) {
// pollRemovedTop(topSmallHeap);
// topLargeHeap.offer(topSmallHeap.poll());
// topSmallHeapSize--;
// topLargeHeapSize++;
// }
// }
//
// public double findMedian() {
// if (Objects.equals(topSmallHeapSize, topLargeHeapSize)) {
// pollRemovedTop(topSmallHeap);
// pollRemovedTop(topLargeHeap);
// return (0.0 + topSmallHeap.peek() + topLargeHeap.peek()) / 2;
// } else {
// pollRemovedTop(topSmallHeap);
// return topSmallHeap.peek();
// }
// }
//
// public int size() {
// return topSmallHeapSize + topLargeHeapSize;
// }
//
// private void pollRemovedTop(PriorityQueue<Integer> heap) {
// if (heap.isEmpty()) {
// return;
// }
// Integer top = heap.peek();
// while (!heap.isEmpty() && counter.containsKey(top)) {
// heap.poll();
// Integer cnt = counter.get(top);
// if (cnt > 1) {
// counter.put(top, cnt - 1);
// } else {
// counter.remove(top);
// }
// top = heap.peek();
// }
// }
// }
// private static class DualHeap {
// private Deque<Integer> heap;
// private int capacity;
// private Map<Integer, Integer> counter;
// private PriorityQueue<Integer> topSmallHeap;
// private PriorityQueue<Integer> topLargeHeap;
// private int topSmallHeapSize;
// private int topLargeHeapSize;
//
// public DualHeap(int capacity) {
// this.capacity = capacity;
// heap = new ArrayDeque<>();
// counter = new HashMap<>();
// topSmallHeap = new PriorityQueue<>();
// topSmallHeapSize = 0;
// topLargeHeap = new PriorityQueue<>((a, b) -> b - a);
// topLargeHeapSize = 0;
// }
//
// public void offer(int val) {
// heap.addLast(val);
// if (heap.size() > capacity) {
// Integer removed = heap.removeFirst();
// counter.put(removed, counter.getOrDefault(removed, 0) + 1);
// int top = getTop(topLargeHeap);
// if (removed <= top) {
// topLargeHeapSize--;
// } else {
// topSmallHeapSize--;
// }
// }
//
// while (topSmallHeapSize > topLargeHeapSize + 1) {
// getTop(topSmallHeap);
// int top = topSmallHeap.poll();
// topLargeHeap.offer(top);
// topLargeHeapSize++;
// topSmallHeapSize--;
// }
//
// while (topLargeHeapSize > topSmallHeapSize) {
// getTop(topLargeHeap);
// Integer top = topLargeHeap.poll();
// topSmallHeap.offer(top);
// topSmallHeapSize++;
// topLargeHeapSize--;
// }
//
// if (topSmallHeapSize == topLargeHeapSize) {
// topLargeHeap.offer(val);
// getTop(topLargeHeap);
// Integer top = topLargeHeap.poll();
// topSmallHeap.offer(top);
// topSmallHeapSize++;
// } else {
// topSmallHeap.offer(val);
// getTop(topSmallHeap);
// int top = topSmallHeap.poll();
// topLargeHeap.offer(top);
// topLargeHeapSize++;
// }
// }
//
// public double findMedian() {
// if (topSmallHeapSize == topLargeHeapSize) {
// int small = getTop(topSmallHeap);
// int large = getTop(topLargeHeap);
// return (0.0 + small + large) / 2;
// } else {
// return getTop(topSmallHeap);
// }
// }
//
// public int size() {
// return heap.size();
// }
//
// private int getTop(PriorityQueue<Integer> heap) {
// int top = heap.peek();
// while (counter.containsKey(top)) {
// heap.poll();
// Integer cnt = counter.get(top);
// if (cnt > 1) {
// counter.put(top, cnt - 1);
// } else {
// counter.remove(top);
// }
// top = heap.peek();
// }
// return top;
// }
// }

