友情支持
如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜
|
|
有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。
公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
304. Range Sum Query 2D - Immutable
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (_row_1, _col_1) and lower right corner (_row_2, _col_2).
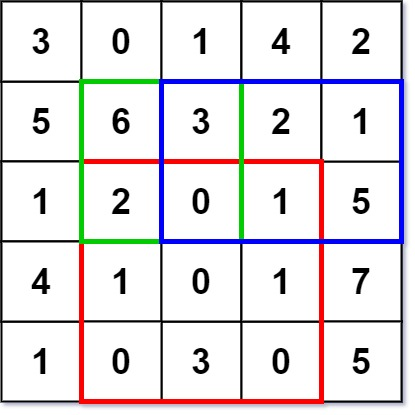
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Example:
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8 // return 8 (红色矩形框的元素总和)
sumRegion(1, 1, 2, 2) -> 11 // return 11 (绿色矩形框的元素总和)
sumRegion(1, 2, 2, 4) -> 12 // return 12 (蓝色矩形框的元素总和)Note:
-
You may assume that the matrix does not change.
-
There are many calls to sumRegion function.
-
You may assume that _row_1 ≤ _row_2 and _col_1 ≤ _col_2.
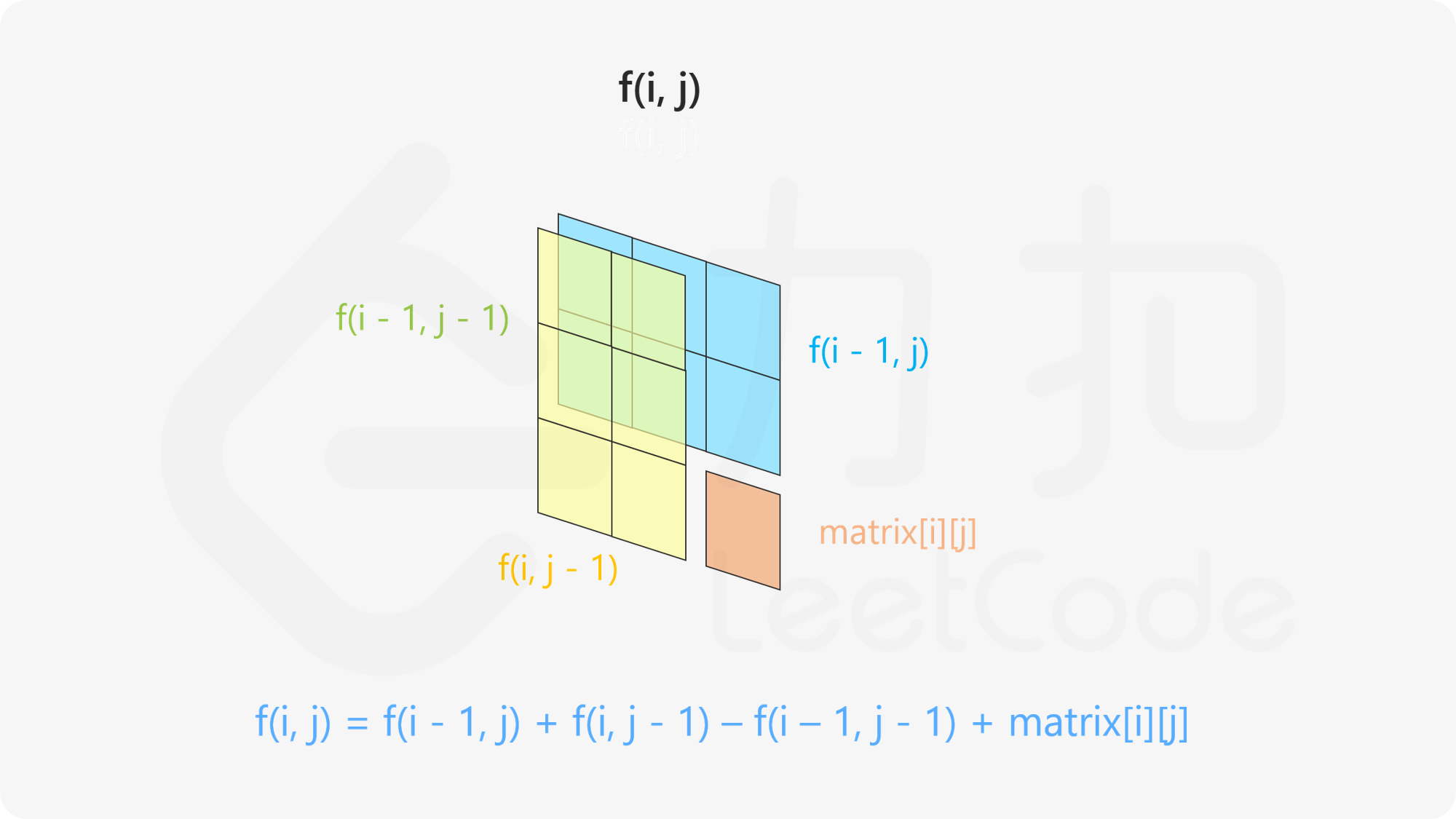
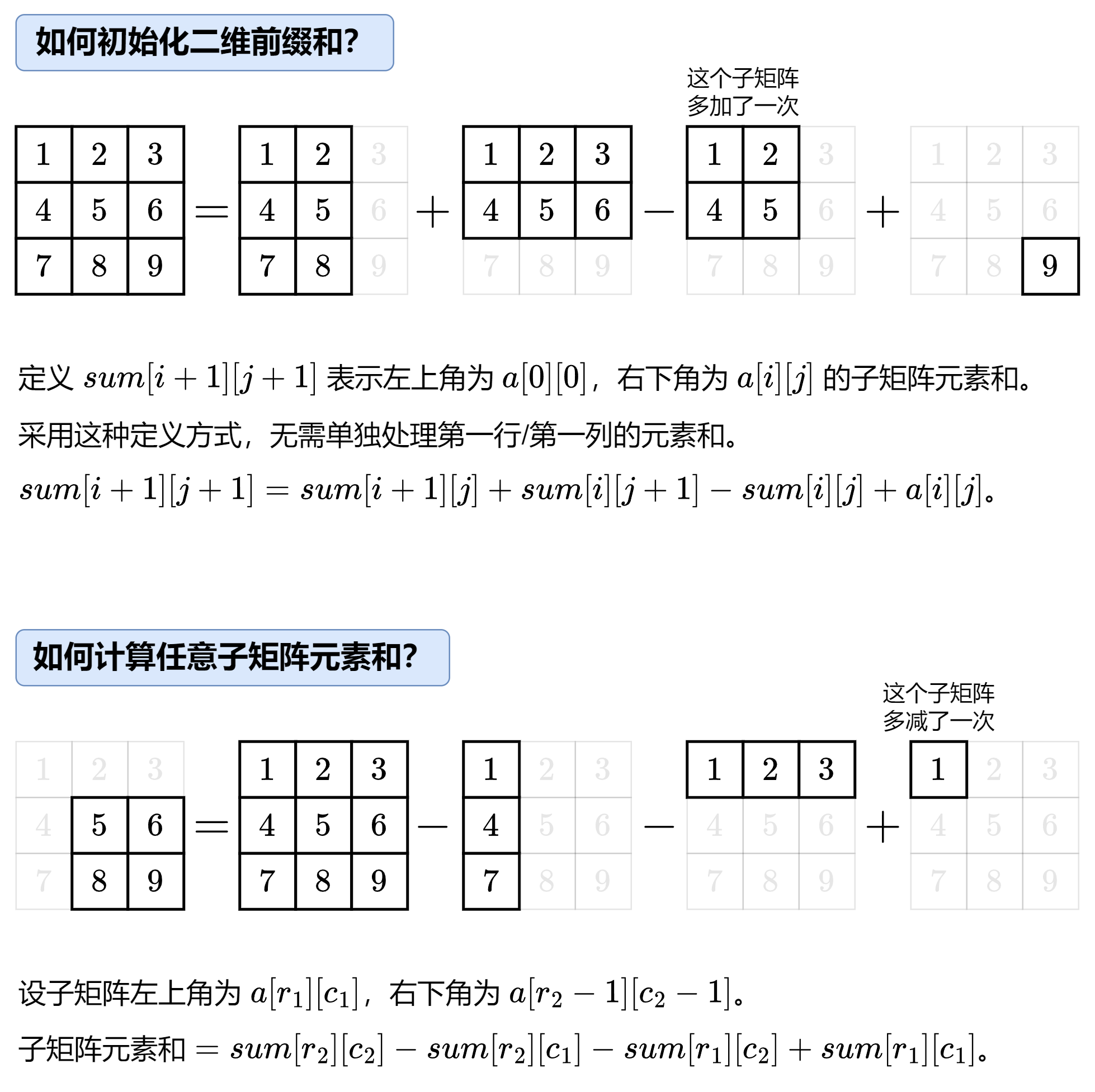
思路分析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
static class NumMatrix {
private int[][] sums;
public NumMatrix(int[][] matrix) {
sums = new int[matrix.length + 1][matrix[0].length + 1];
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
if (i == 0) {
sums[i + 1][j + 1] = sums[i + 1][j] + matrix[i][j];
} else if (j == 0) {
sums[i + 1][j + 1] = sums[i][j + 1] + matrix[i][j];
} else {
sums[i + 1][j + 1] = sums[i + 1][j]
+ sums[i][j + 1] + matrix[i][j] - sums[i][j];
}
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return sums[row2 + 1][col2 + 1] - sums[row2 + 1][col1]
- sums[row1][col2 + 1] + sums[row1][col1];
}
}