友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
370. 区间加法
假设你有一个长度为 n 的数组,初始情况下所有的数字均为 0,你将会被给出 k 个更新的操作。
其中,每个操作会被表示为一个三元组:[startIndex, endIndex, inc],表示需要将子数组 A[startIndex … endIndex](含 startIndex 和 endIndex)增加 inc。
请你返回 k 次操作后的数组。
示例:
输入:
length = 5,
updates = [
[1, 3, 2],
[2, 4, 3],
[0, 2, -2]
]
输出: [-2,0,3,5,3]
解释:
初始状态: [0,0,0,0,0] 进行了操作 [1,3,2] 后的状态: [0,2,2,2,0] 进行了操作 [2,4,3] 后的状态: [0,2,5,5,3] 进行了操作 [0,2,-2] 后的状态: [-2,0,3,5,3]
思路分析
差分数组:把变量记录在差分数组上进行打标,全部打标完成后,再从第二项开始逐项求与前一项的累加值。
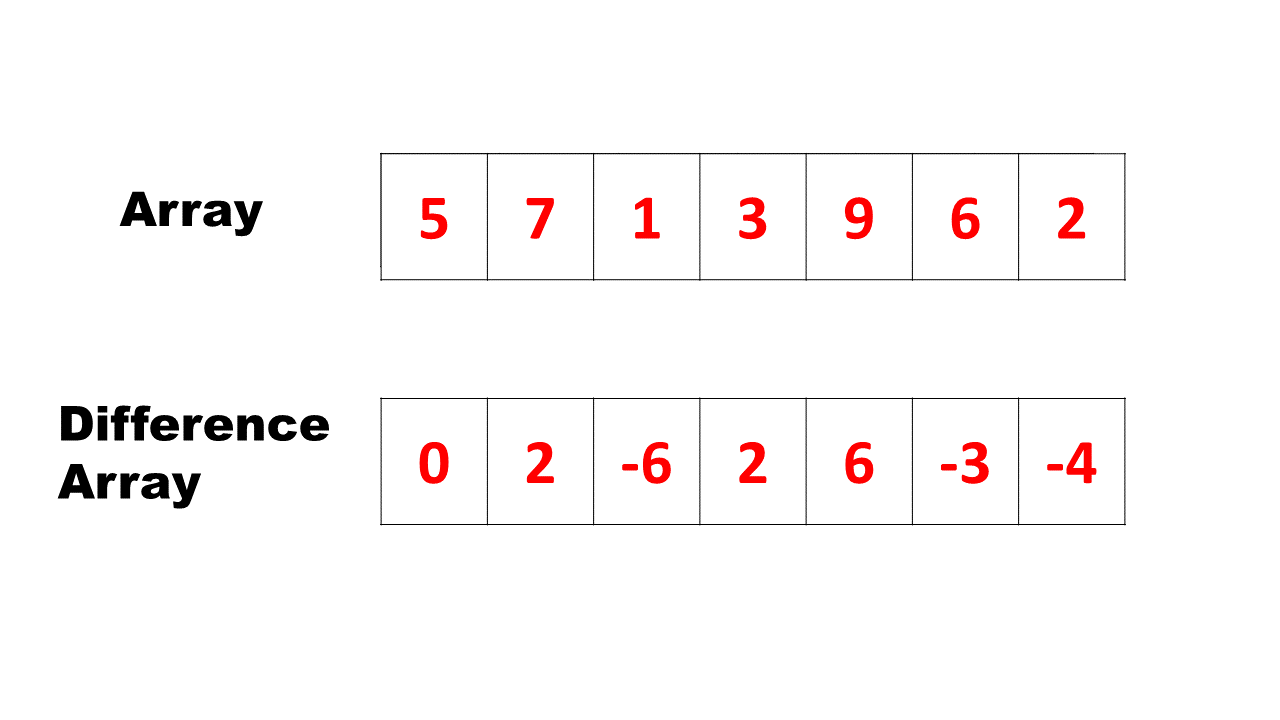
这道题与 1094. 拼车 一样,并且它不是 Plus 题目,可以验证答案。
-
一刷
-
二刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2024-07-05 14:39:13
*/
public int[] getModifiedArray(int length, int[][] updates) {
if (updates == null || updates.length == 0) {
return new int[length];
}
int[] diff = new int[length];
for (int[] update : updates) {
int start = update[0];
int end = update[1];
int val = update[2];
diff[start] += val;
if (end + 1 < diff.length) {
diff[end + 1] -= val;
}
}
for (int i = 1; i < length; i++) {
diff[i] += diff[i - 1];
}
return diff;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-09-07 17:47:44
*/
public int[] getModifiedArray(int length, int[][] updates) {
int[] array = new int[length];
for (int[] update : updates) {
int start = update[0];
int end = update[1];
int value = update[2];
array[start] += value;
if (end + 1 < length) {
array[end + 1] -= value;
}
}
for (int i = 1; i < length; i++) {
array[i] += array[i - 1];
}
return array;
}

