友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
Dynamic Programming 动态规划
动态规划的设计思想:「不是直接面对问题求解,而是从一个最小规模的问题开始,新问的最优解均是由比它规模还小的子问题的最优解转换得到,在求解的过程中记录每一步的结果,直至所要求的问题得到解」。
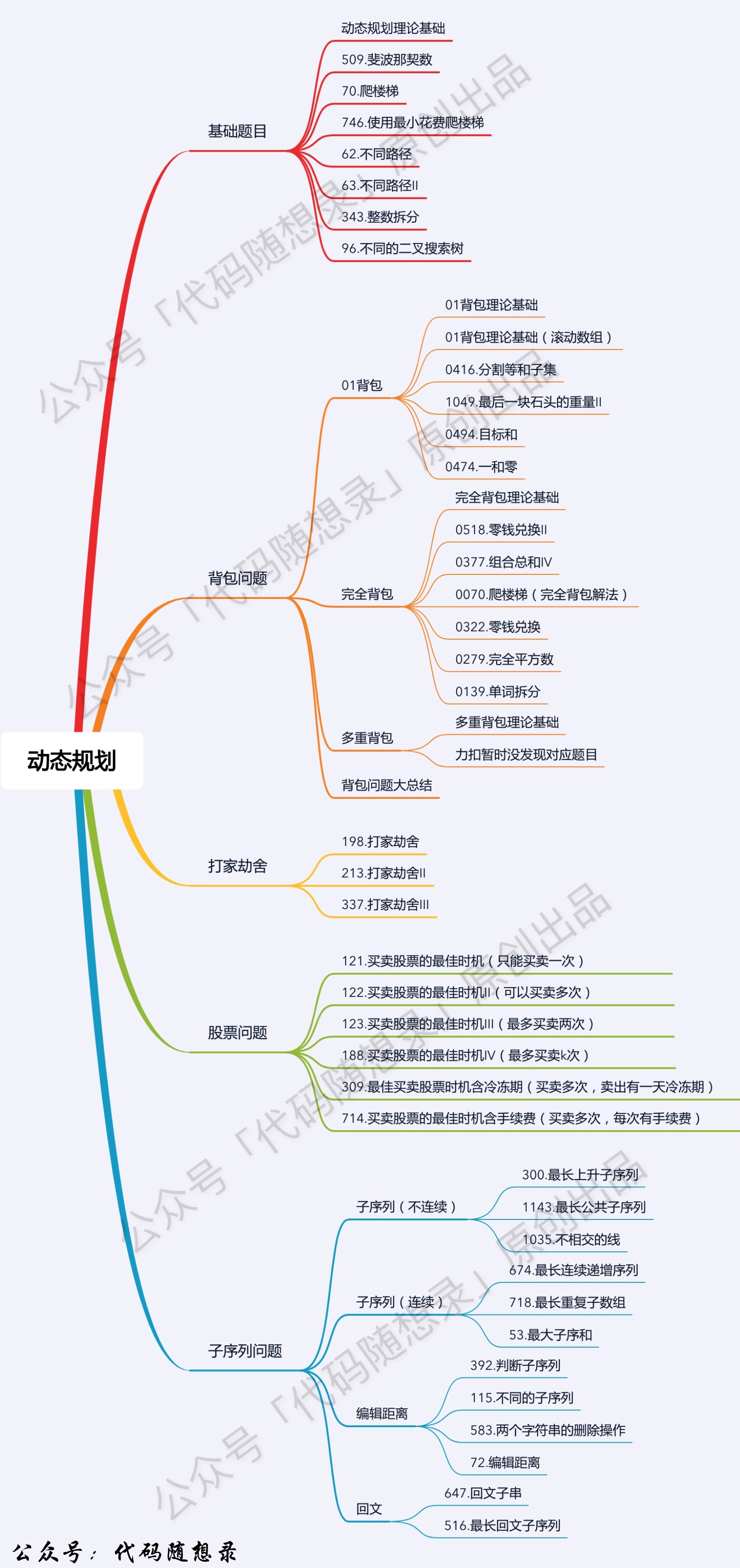
动态规划的五部曲:
-
确定 dp 数组(dp table)以及下标的含义
-
确定递推公式
-
dp 数组如何初始化
-
确定遍历顺序
-
举例推导 dp 数组
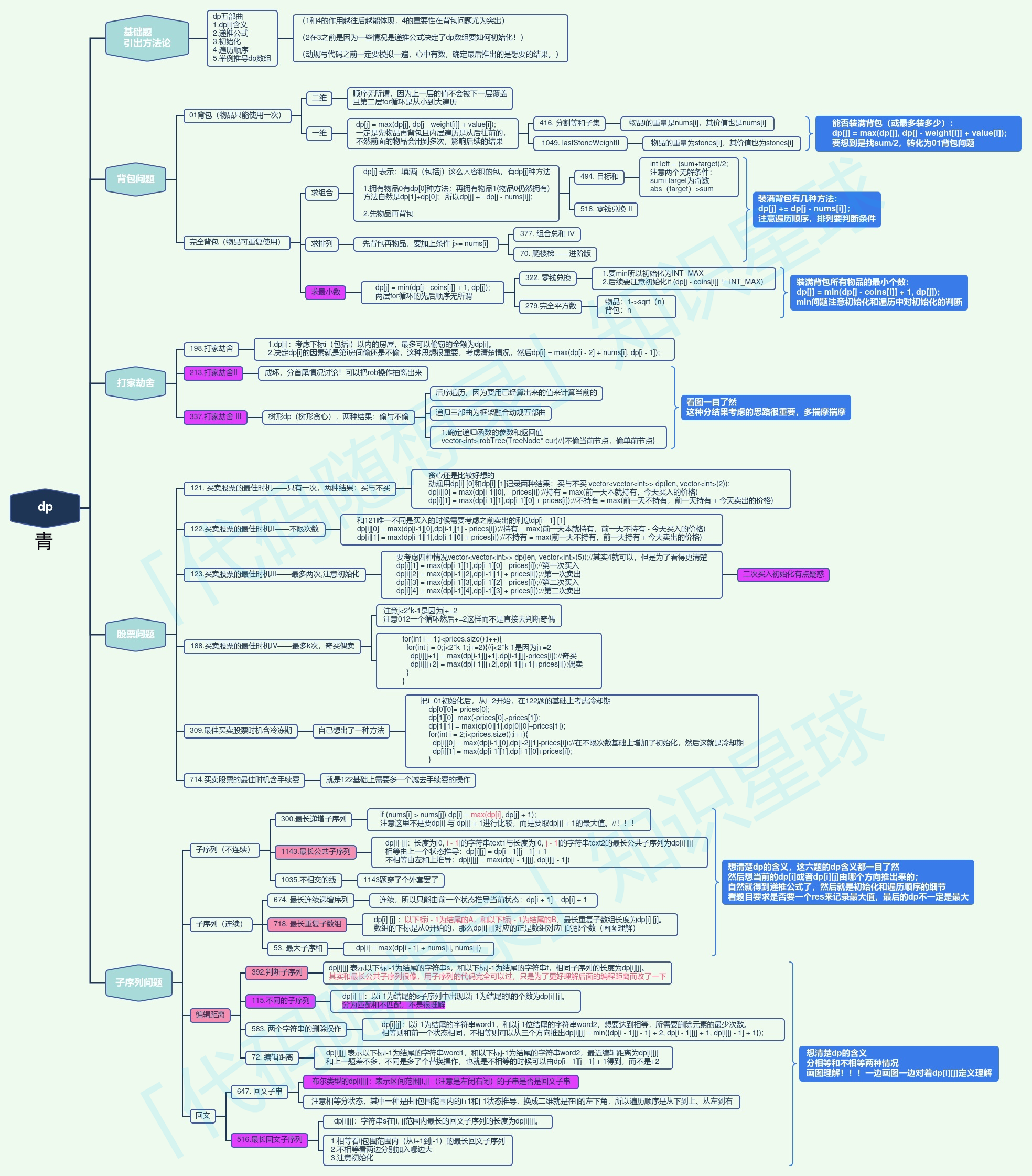
.1. 题目类型
.2. 0/1 Knapsack 0/1 背包
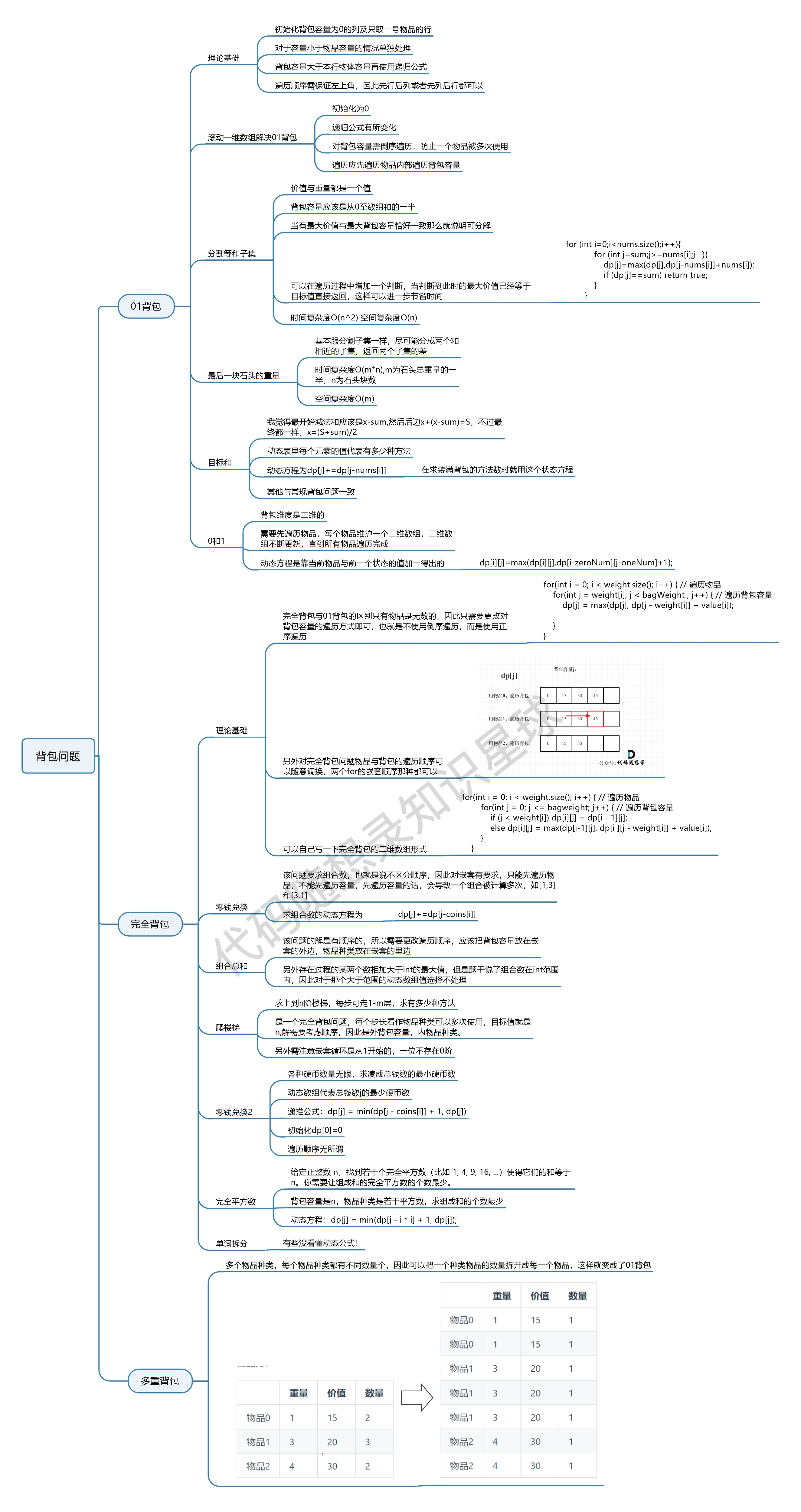
.3. Unbounded Knapsack 完全背包
416. 分割等和子集 与 322. 零钱兑换 对比,体会一下 0/1 Knapsack 0/1 背包 与 Unbounded Knapsack 完全背包 的差异:
| 特征 | 0/1 背包 (0/1 Knapsack) | 完全背包 (Unbounded Knapsack) |
|---|---|---|
核心定义 |
每种物品仅有一件 |
每种物品有无限件 |
二维状态转移方程 |
\$dp[i][j] = max(dp[i-1][j], dp[i-1][j-w]+v)\$ |
\$dp[i][j] = max(dp[i-1][j], dp[i][j-w]+v)\$ |
状态依赖 |
依赖上一轮 ( |
依赖本轮 ( |
一维优化遍历顺序 |
逆序遍历背包容量 |
正序遍历背包容量 |
Java核心代码差异 |
|
|
.3.1. 经典题目
Unbounded Knapsack,无限背包
Rod Cutting,切钢条问题
Minimum Coin Change,凑齐每个数需要的最少硬币问题
Maximum Ribbon Cut,丝带的最大值切法
.4. Fibonacci Numbers 斐波那契数列
.5. Palindromic Subsequence 回文子系列
.6. Longest Common Substring 最长子字符串系列
对比 718. 最长重复子数组 和 1143. 最长公共子序列 两道题的差异:
-
对于求子数组来说:
-
使用深度优先遍历的暴力破解方法,当不符合子数组约束时,递归被终止。如果只用一个入口无法覆盖全部场景,必须使用循环尝试多个入口才能覆盖掉。
-
使用动态规划时,只需要更新符合条件的情况即可,其他情况无需更新。
-
-
对于求子序列来讲:
-
使用深度优先遍历的暴力破解方法,不会中间终止,递归过程会覆盖全部场景,所以,只需要一个入口即可。
-
使用动态规划时,每一个节点都是前一个节点的累加或者两个节点的最大值,所以,任何情况都需要更新。
-
.6.1. 经典题目
Longest Common Substring,最长相同子串
Longest Common Subsequence,最长相同子序列
Minimum Deletions & Insertions to Transform a String into another,字符串变换
Longest Increasing Subsequence,最长上升子序列
Maximum Sum Increasing Subsequence,最长上升子序列和
Shortest Common Super-sequence,最短超级子序列
Minimum Deletions to Make a Sequence Sorted,最少删除变换出子序列
Longest Repeating Subsequence,最长重复子序列
Subsequence Pattern Matching,子序列匹配
Longest Bitonic Subsequence,最长字节子序列
Longest Alternating Subsequence,最长交差变换子序列
Edit Distance,编辑距离
Strings Interleaving,交织字符串
.7. 树形 DP 套路
树形 DP 套路使用前提:如果题目求解目标是 S 规则,则求解释流程可以定成以每一个节点为头节点的子树在 S 规则下的每一个答案,并且最终答案一定就在其中。
树形 DP 套路的解题步骤
-
第一步:以某个节点 X 为头节点的子树中,分析答案有哪些可能性,并且这种分析是以 X 的左子树、X 的右子树和 X 整棵树的角度来考虑可能性的。
请注意这里的顺序:左子树、右子树及整棵树。先左右,如果左右满足,则就可以先上延伸,判断出整棵树。这也是递归调用“触底反弹”的过程。所以,很容易使用递归来完成相关操作。根据上述的流程,使用 后序遍历 更合适。 -
第二步:根据第一步的可能性分析,列出所有需要的信息。比如:最大值、最小值,高度,深度,节点数等等。
-
第三步:合并第二步的信息,对左树和右树提出同样的要求,并写出信息结构。
写出信息结构是把所有的信息都装到一个对象中。如果只需要一个信息,就可以用简单类型来表示了。但是,在树的结构中,大概率是需要多个信息的。 -
第四步:设计递归函数,递归函数是处理以 X 为头节点的情况下的大难,包括设计递归的 base case,默认直接得到左树和右树的所有信息,以及把可能性做整合,并且要返回第三步的信息结构。
.8. 经典题目
.8.1. 入门题目
.8.1.1. 类型排序
-
2560. 打家劫舍 IV — 这个不是动态规划题目。
-
980. 不同路径 III — 这是一道回溯问题。
-
140. 单词拆分 II — 这是一道回溯题。
-
[1964-find-the-longest-valid-obstacle-course-at-each-position]
.8.1.2. 题号排序
-
140. 单词拆分 II — 这是一道回溯题。
-
980. 不同路径 III — 这是一道回溯问题。
-
[1964-find-the-longest-valid-obstacle-course-at-each-position]
-
2560. 打家劫舍 IV — 这个不是动态规划题目。
.8.2. 进阶
.8.2.1. 类型排序
.8.3. 经典题目
-
[0828-count-unique-characters-of-all-substrings-of-a-given-string]
-
[1269-number-of-ways-to-stay-in-the-same-place-after-some-steps]
-
[1334-find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance]
-
[1420-build-array-where-you-can-find-the-maximum-exactly-k-comparisons]
-
[1449-form-largest-integer-with-digits-that-add-up-to-target]
-
[1467-probability-of-a-two-boxes-having-the-same-number-of-distinct-balls]
-
[1477-find-two-non-overlapping-sub-arrays-each-with-target-sum]
-
[1526-minimum-number-of-increments-on-subarrays-to-form-a-target-array]
-
[1639-number-of-ways-to-form-a-target-string-given-a-dictionary]
-
[1770-maximum-score-from-performing-multiplication-operations]
-
[1866-number-of-ways-to-rearrange-sticks-with-k-sticks-visible]
-
[1888-minimum-number-of-flips-to-make-the-binary-string-alternating]
-
[1959-minimum-total-space-wasted-with-k-resizing-operations]
-
[1981-minimize-the-difference-between-target-and-chosen-elements]
-
[2002-maximum-product-of-the-length-of-two-palindromic-subsequences]
-
[2035-partition-array-into-two-arrays-to-minimize-sum-difference]
-
[2060-check-if-an-original-string-exists-given-two-encoded-strings]
-
[2167-minimum-time-to-remove-all-cars-containing-illegal-goods]
-
[2400-number-of-ways-to-reach-a-position-after-exactly-k-steps]
-
[2436-minimum-split-into-subarrays-with-gcd-greater-than-one]
-
[2472-maximum-number-of-non-overlapping-palindrome-substrings]
-
[2510-check-if-there-is-a-path-with-equal-number-of-0s-and-1s]
-
[2522-partition-string-into-substrings-with-values-at-most-k]
-
[2556-disconnect-path-in-a-binary-matrix-by-at-most-one-flip]
-
[2892-minimizing-array-after-replacing-pairs-with-their-product]
-
[2915-length-of-the-longest-subsequence-that-sums-to-target]
-
[2930-number-of-strings-which-can-be-rearranged-to-contain-substring]
-
[3007-maximum-number-that-sum-of-the-prices-is-less-than-or-equal-to-k]
-
[3018-maximum-number-of-removal-queries-that-can-be-processed-i]
-
[3041-maximize-consecutive-elements-in-an-array-after-modification]
-
[3135-equalize-strings-by-adding-or-removing-characters-at-ends]
-
[3144-minimum-substring-partition-of-equal-character-frequency]
-
[3165-maximum-sum-of-subsequence-with-non-adjacent-elements]
-
[3192-minimum-operations-to-make-binary-array-elements-equal-to-one-ii]
-
[3389-minimum-operations-to-make-character-frequencies-equal]
-
[3409-longest-subsequence-with-decreasing-adjacent-difference]
-
[3410-maximize-subarray-sum-after-removing-all-occurrences-of-one-element]
-
[3428-maximum-and-minimum-sums-of-at-most-size-k-subsequences]
-
[3472-longest-palindromic-subsequence-after-at-most-k-operations]
-
[3505-minimum-operations-to-make-elements-within-k-subarrays-equal]

