LeetCode: 115. 不同的子序列

友情支持

如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜

支付宝

有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。

wx jikerizhi

公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。

115. 不同的子序列

LeetCode - 115. 不同的子序列

给你两个字符串 s * 和 t ，统计并返回在 s 的 *子序列中 t 出现的个数。

测试用例保证结果在 32 位有符号整数范围内。

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

示例 2：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag

提示：

1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成

思路分析

首先想到的思路是回溯，可惜在通过 52 / 66 个测试用例后，开始超时。

看题解，可以使用动态规划的思路来解题。

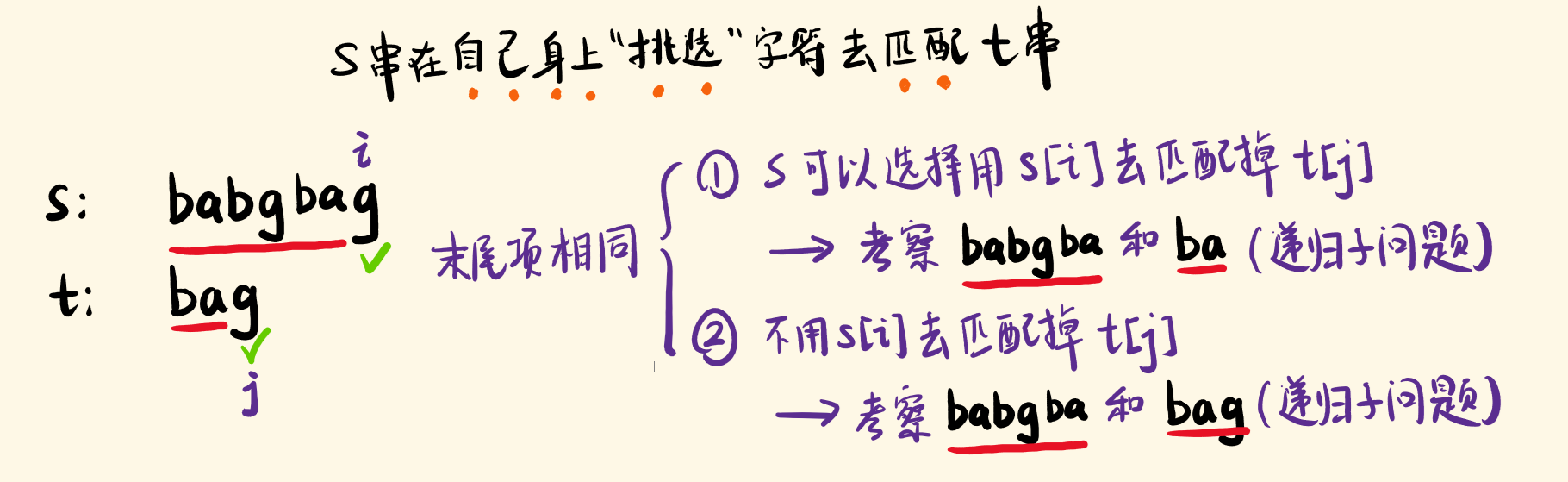
题目可以理解成，从 s[0..i] 中去匹配 t[0..j]。分两种情况考虑：

当 s[i] == t[j] 时，可以从 s[i] 和 s[i-1] 中去寻找 t[j]；
当 s[i] != t[j] 时，只能从 s[i-1] 中去寻找 t[j]。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * 超时，通过 52 / 66 个测试用例。
 *
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-05-02 21:46:40
 */
public int numDistinct(String s, String t) {
  Set<List<Integer>> result = new HashSet<>();
  List<Integer> path = new ArrayList<>(t.length());
  backtrack(s, t, result, path, 0, 0);
  return result.size();
}

private void backtrack(String s, String t,
                       Set<List<Integer>> result, List<Integer> path,
                       int originIndex, int subIndex) {
  if (subIndex == t.length()) {
    result.add(new ArrayList<>(path));
    return;
  }
  for (int i = originIndex; i < s.length(); i++) {
    if (s.length() - i < t.length() - subIndex) {
      return;
    }
    if (s.charAt(i) != t.charAt(subIndex)) {
      continue;
    }
    path.add(i);
    backtrack(s, t, result, path, i + 1, subIndex + 1);
    path.removeLast();
  }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-05-02 22:07:01
 */
public int numDistinct(String s, String t) {
  int m = s.length(), n = t.length();
  if (m < n) {
    return 0;
  }
  // dp[i][j] 在 s[0..i] 中可以匹配多少个 t[0..j]
  int[][] dp = new int[m + 1][n + 1];
  // 在 t 的长度为 0 时，需要删除所有 s 才能匹配一个 t
  for (int i = 0; i <= m; i++) {
    dp[i][0] = 1;
  }
  for (int i = 1; i <= m; i++) {
    // 之所以 j <= i，是因为，如果 t 的长度大于 s，则必然没有子序列
    for (int j = 1; j <= i && j <= n; j++) {
      // 如果 s[i] != t[j]，那么只能在 s[i-1] 中查找 t[j]
      dp[i][j] = dp[i - 1][j];
      // 如果 s[i] == t[j]，则 可以在 s[i] 和 s[i-1] 中查找 t[j]
      if (s.charAt(i - 1) == t.charAt(j - 1)) {
        dp[i][j] += dp[i - 1][j - 1];
      }
    }
  }
  return dp[m][n];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * 暴力破解（55/66）
 * @author D瓜哥 · https://www.diguage.com
 * @since 2026-01-15 09:22:47
 */
public int numDistinct(String s, String t) {
  return dfs(s.toCharArray(), s.length() - 1, t.toCharArray(), t.length() - 1);
}

private int dfs(char[] s, int si, char[] t, int ti) {
  // 如果目标字符串的长度为 0，则只有一种方式
  if (ti < 0) {
    return 1;
  }
  // 如果来源字符串为 0，则无法组成目标字符串
  if (si < 0) {
    return 0;
  }
  int result = dfs(s, si - 1, t, ti);
  if (s[si] == t[ti]) {
    result += dfs(s, si - 1, t, ti - 1);
  }
  return result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * 暴力破解（55/66） -> 备忘录（6.33%）
 *
 * @author D瓜哥 · https://www.diguage.com
 * @since 2026-01-15 10:10:17
 */
public int numDistinct(String s, String t) {
  int[][] memo = new int[s.length()][t.length()];
  for (int[] ints : memo) {
    Arrays.fill(ints, -1);
  }
  return dfs(s.toCharArray(), s.length() - 1, t.toCharArray(), t.length() - 1, memo);
}

private int dfs(char[] s, int si, char[] t, int ti, int[][] memo) {
  // 如果目标字符串的长度为 0，则只有一种方式
  if (ti < 0) {
    return 1;
  }
  // 如果来源字符串为 0，则无法组成目标字符串
  if (si < 0) {
    return 0;
  }
  if (memo[si][ti] >= 0) {
    return memo[si][ti];
  }
  int result = dfs(s, si - 1, t, ti, memo);
  if (s[si] == t[ti]) {
    result += dfs(s, si - 1, t, ti - 1, memo);
  }
  return memo[si][ti] = result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * 暴力破解（55/66） -> 备忘录（6.33%）-> 动态规划
 *
 * @author D瓜哥 · https://www.diguage.com
 * @since 2026-01-15 19:44:24
 */
public int numDistinct(String s, String t) {
  int m = s.length();
  int n = t.length();
  int[][] dp = new int[n + 1][m + 1];
  Arrays.fill(dp[0], 1);
  char[] scs = s.toCharArray();
  char[] tcs = t.toCharArray();
  for (int ti = 1; ti <= n; ti++) {
    for (int si = ti; si <= m; si++) {
      dp[ti][si] = dp[ti][si - 1];
      if (scs[si - 1] == tcs[ti - 1]) {
        dp[ti][si] += dp[ti - 1][si - 1];
      }
    }
  }
  return dp[n][m];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2026-01-14 20:21:39
 */
public int numDistinct(String s, String t) {
  int m = s.length();
  int n = t.length();
  int[][] dp = new int[m + 1][n + 1];
  // 当 t 的长度为 0 时，则只有一种组成方式
  for (int i = 0; i <= m; i++) {
    dp[i][0] = 1;
  }
  char[] tcs = t.toCharArray();
  char[] scs = s.toCharArray();
  for (int ti = 1; ti <= n; ti++) {
    char tc = tcs[ti - 1];
    for (int si = 1; si <= m; si++) {
      char sc = scs[si - 1];
      dp[si][ti] = dp[si - 1][ti];
      if (tc == sc) {
        dp[si][ti] += dp[si - 1][ti - 1];
      }
    }
  }
  return dp[m][n];
}

LeetCode: 115. 不同的子序列

友情支持

115. 不同的子序列

思路分析

参考资料