LeetCode: 718. 最长重复子数组

友情支持

如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜

支付宝

有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。

wx jikerizhi

公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。

718. 最长重复子数组

LeetCode - 718. 最长重复子数组

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的、长度最长的子数组的长度。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100

思路分析

该题的暴力破解解法可以看出，深度优先遍历不一定都能从一个入口遍历完，可能还需要多个入口。

动态规划：

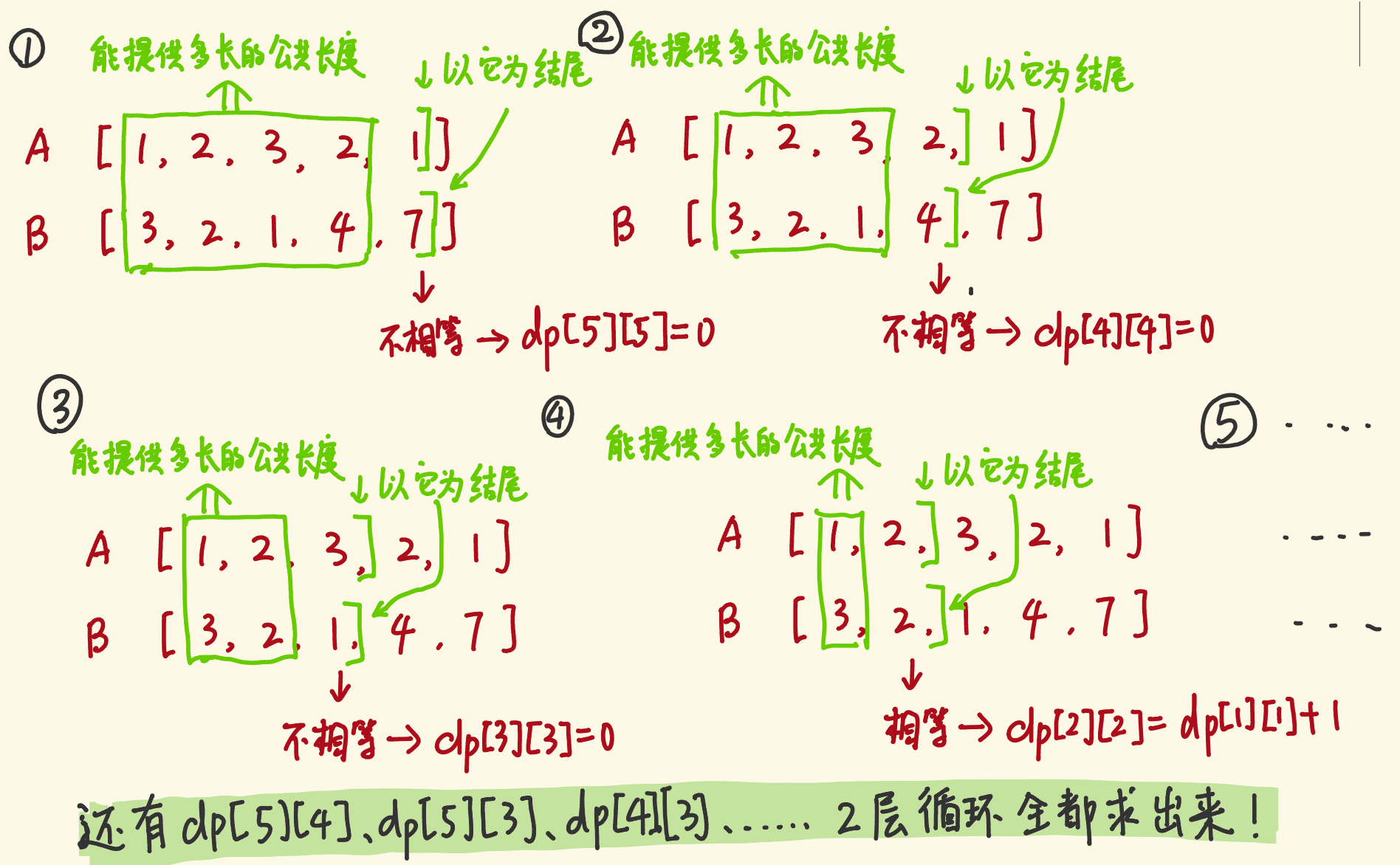
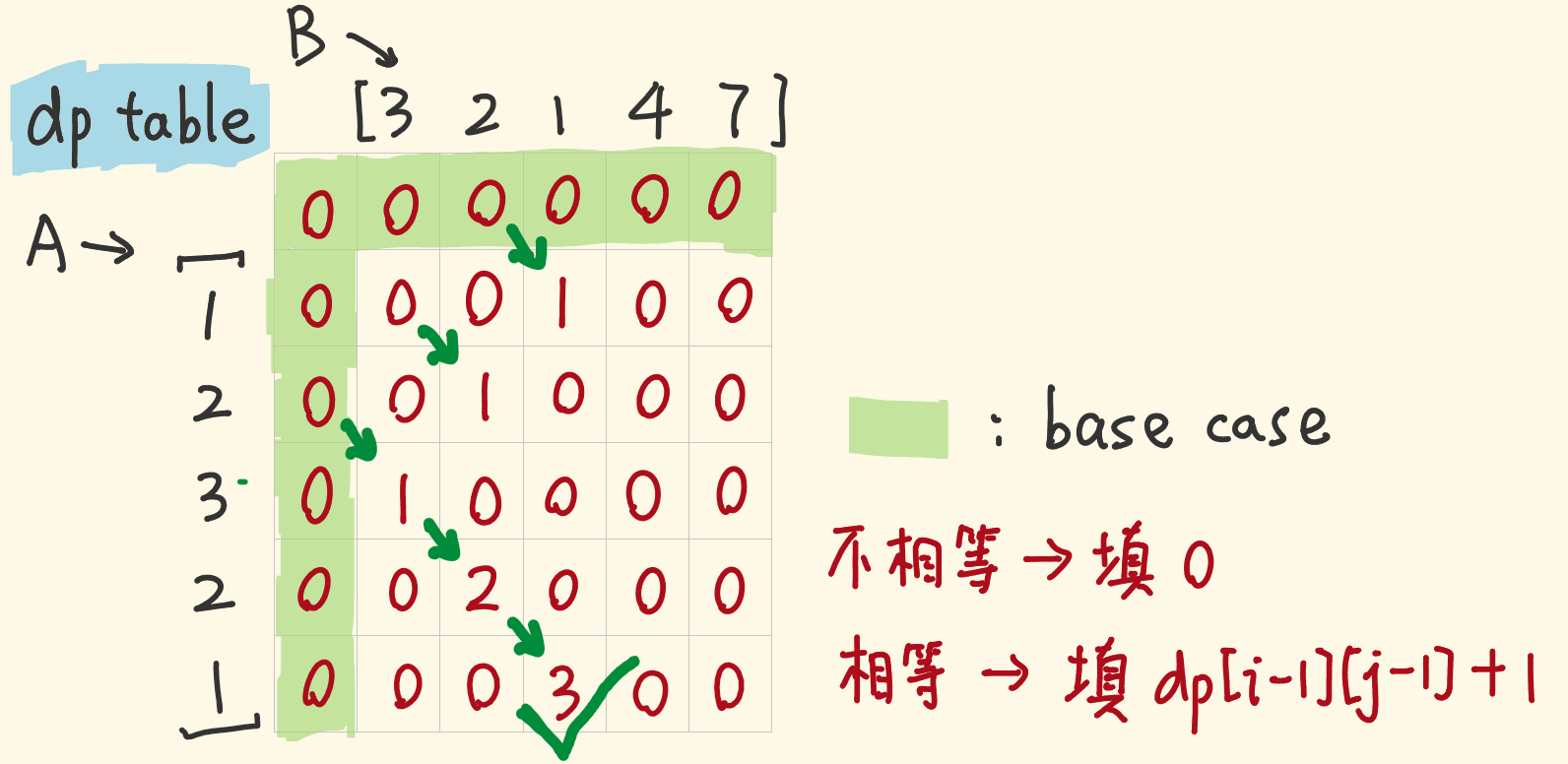
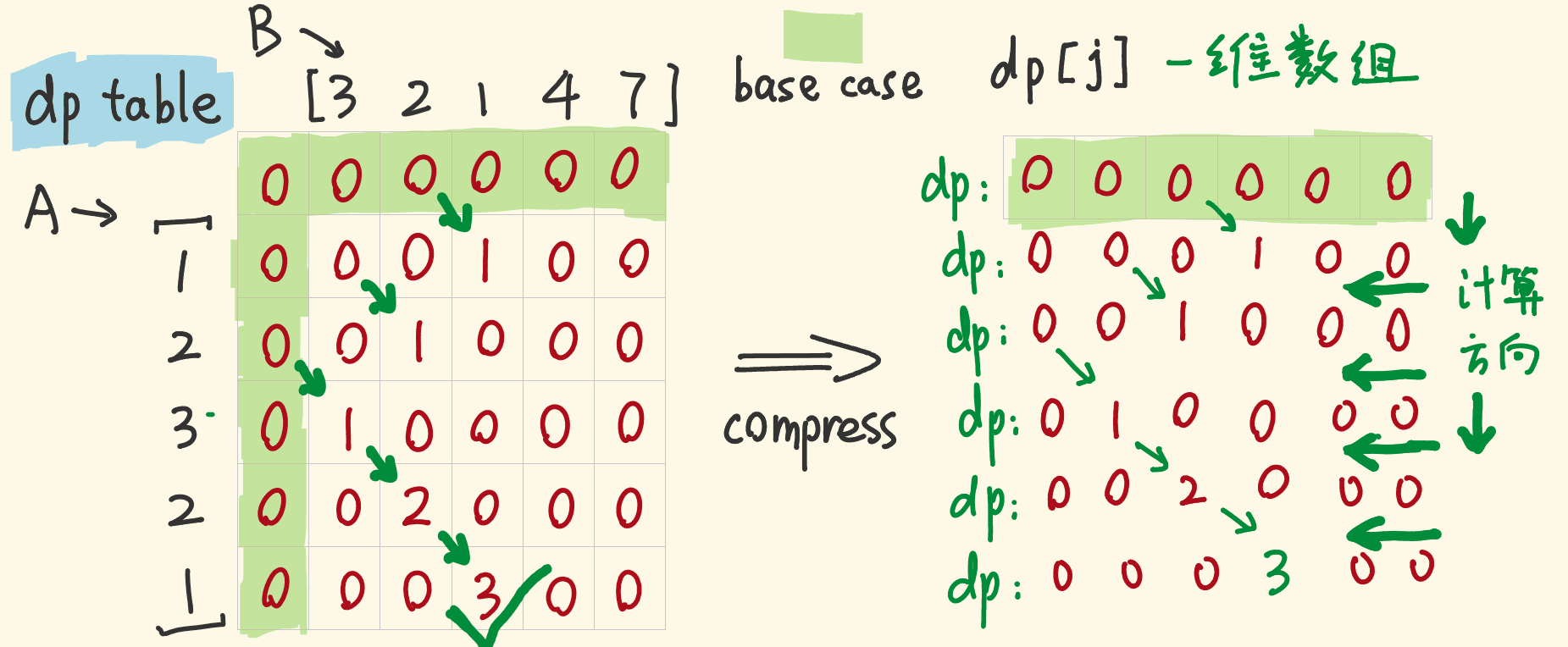
这里求的是公共子数组，只能在两个字符相等时，在上一个字符的基础上加 1，否则就应该设置为 0。不能取 min{dp[i-1][j], dp[i][j-1]}。

对比 1143. 最长公共子序列，注意区分“子数组”和“子序列”的区别。

对比 718. 最长重复子数组和 1143. 最长公共子序列两道题的差异：

对于求子数组来说：
1. 使用深度优先遍历的暴力破解方法，当不符合子数组约束时，递归被终止。如果只用一个入口无法覆盖全部场景，必须使用循环尝试多个入口才能覆盖掉。
2. 使用动态规划时，只需要更新符合条件的情况即可，其他情况无需更新。
对于求子序列来讲：
1. 使用深度优先遍历的暴力破解方法，不会中间终止，递归过程会覆盖全部场景，所以，只需要一个入口即可。
2. 使用动态规划时，每一个节点都是前一个节点的累加或者两个节点的最大值，所以，任何情况都需要更新。

滑动窗口的解法非常妙！

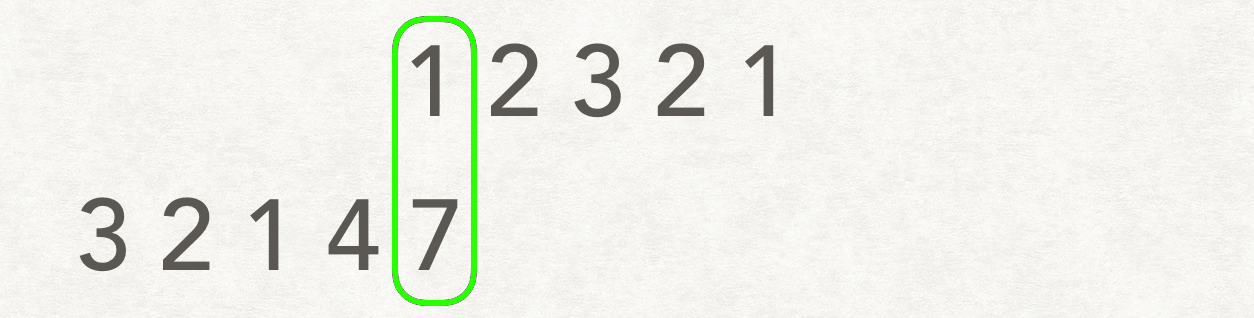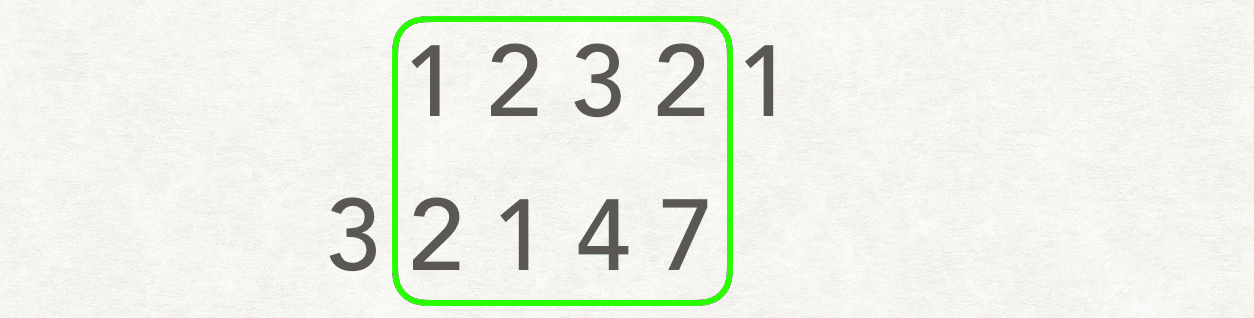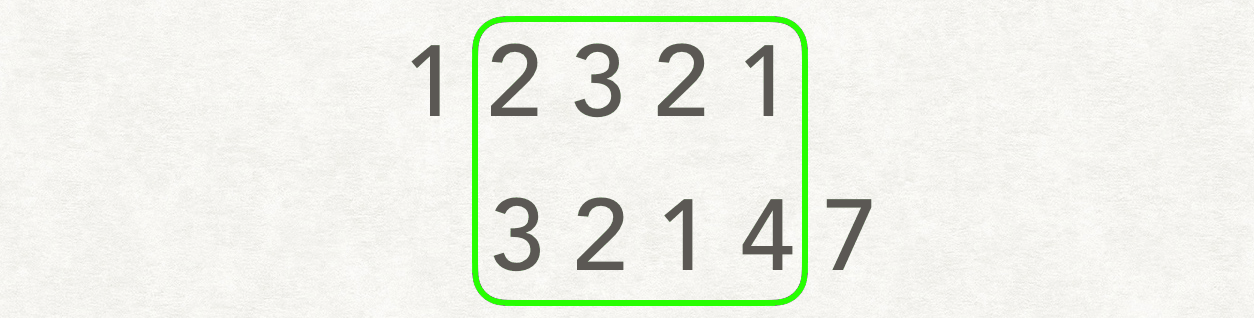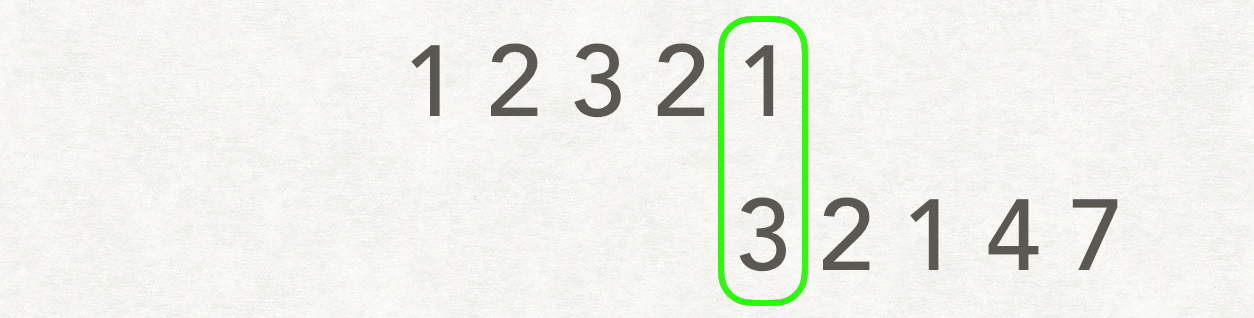
0718 01

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2024-09-30 20:18:46
 */
public int findLength(int[] nums1, int[] nums2) {
  int n = nums1.length, m = nums2.length;
  int[][] dp = new int[n + 1][m + 1];
  int result = 0;
  for (int i = n - 1; i >= 0; i--) {
    for (int j = m - 1; j >= 0; j--) {
      dp[i][j] = nums1[i] == nums2[j] ? dp[i + 1][j + 1] + 1 : 0;
      result = Math.max(result, dp[i][j]);
    }
  }
  return result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-04-21 19:55:47
 */
public int findLength(int[] nums1, int[] nums2) {
  int m = nums1.length, n = nums2.length;
  int[][] dp = new int[m + 1][n + 1];
  int result = 0;
  for (int i = 1; i <= m; i++) {
    for (int j = 1; j <= n; j++) {
      // 只有在必要的时候采取更新 dp[i][j] 和 result
      // 简化一下，效率提高很多。
      if (nums1[i - 1] == nums2[j - 1]) {
        // 默认就是 0 ，则不需要再次设置为 0
        // ac == bc ? dp[i - 1][j - 1] + 1 : 0
        dp[i][j] = dp[i - 1][j - 1] + 1;
        result = Math.max(result, dp[i][j]);
      }
    }
  }
  return result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-12-29 19:28:31
 */
public int findLength(int[] nums1, int[] nums2) {
  int result = 0;
  for (int i = 0; i < nums1.length; i++) {
    result = Math.max(result, findLength(nums1, i, nums2, 0));
  }
  for (int i = 1; i < nums2.length; i++) {
    result = Math.max(result, findLength(nums1, 0, nums2, i));
  }
  return result;
}

private int findLength(int[] a, int ai, int[] b, int bi) {
  int result = 0;
  int temp = 0;
  while (ai < a.length && bi < b.length) {
    if (a[ai] == b[bi]) {
      temp++;
    } else {
      temp = 0;
    }
    result = Math.max(result, temp);
    ai++;
    bi++;
  }
  return result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * 暴力破解（42/55）
 *
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-12-29 19:53:46
 */
public int findLength(int[] nums1, int[] nums2) {
  int result = 0;
  // 从这里也可以看出，深度优先遍历不一定都能从一个入口遍历完，可能还需要多个入口。
  for (int i = nums1.length - 1; i >= 0; i--) {
    for (int j = nums2.length - 1; j >= 0; j--) {
      result = Math.max(result, dfs(nums1, i, nums2, j));
    }
  }
  return result;
}

private int dfs(int[] a, int ai, int[] b, int bi) {
  if (ai < 0 || bi < 0) {
    return 0;
  }
  if (a[ai] == b[bi]) {
    return dfs(a, ai - 1, b, bi - 1) + 1;
  } else {
    return 0;
  }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * 暴力破解（42/55）→ 备忘录
 *
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-12-29 19:53:46
 */
public int findLength(int[] nums1, int[] nums2) {
  int result = 0;
  int[][] memo = new int[nums1.length][nums2.length];
  for (int[] ints : memo) {
    Arrays.fill(ints, -1);
  }
  for (int i = nums1.length - 1; i >= 0; i--) {
    for (int j = nums2.length - 1; j >= 0; j--) {
      result = Math.max(result, dfs(nums1, i, nums2, j, memo));
    }
  }
  return result;
}

private int dfs(int[] a, int ai, int[] b, int bi, int[][] memo) {
  if (ai < 0 || bi < 0) {
    return 0;
  }
  if (memo[ai][bi] >= 0) {
    return memo[ai][bi];
  }
  int result = 0;
  if (a[ai] == b[bi]) {
    result = dfs(a, ai - 1, b, bi - 1, memo) + 1;
  }
  memo[ai][bi] = result;
  return result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
/**
 * 暴力破解（42/55）→ 备忘录（5.22%）→ 动态规划
 *
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-12-29 19:53:46
 */
public int findLength(int[] nums1, int[] nums2) {
  int result = 0;
  int[][] dp = new int[nums1.length + 1][nums2.length + 1];
  for (int i = 0; i < nums1.length; i++) {
    for (int j = 0; j < nums2.length; j++) {
      if (nums1[i] == nums2[j]) {
        dp[i + 1][j + 1] = dp[i][j] + 1;
        result = Math.max(result, dp[i + 1][j + 1]);
      }
    }
  }
  return result;
}

LeetCode: 718. 最长重复子数组

友情支持

718. 最长重复子数组

思路分析

参考资料