友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
11. 盛最多水的容器
给定一个长度为 n 的整数数组 height。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i])。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
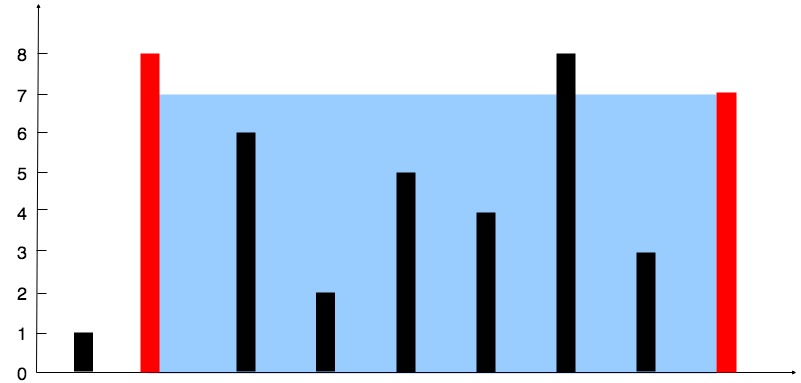
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。
在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
提示:
-
n == height.length -
2 <= n <= 105 -
0 <= height[i] <= 104
解题分析
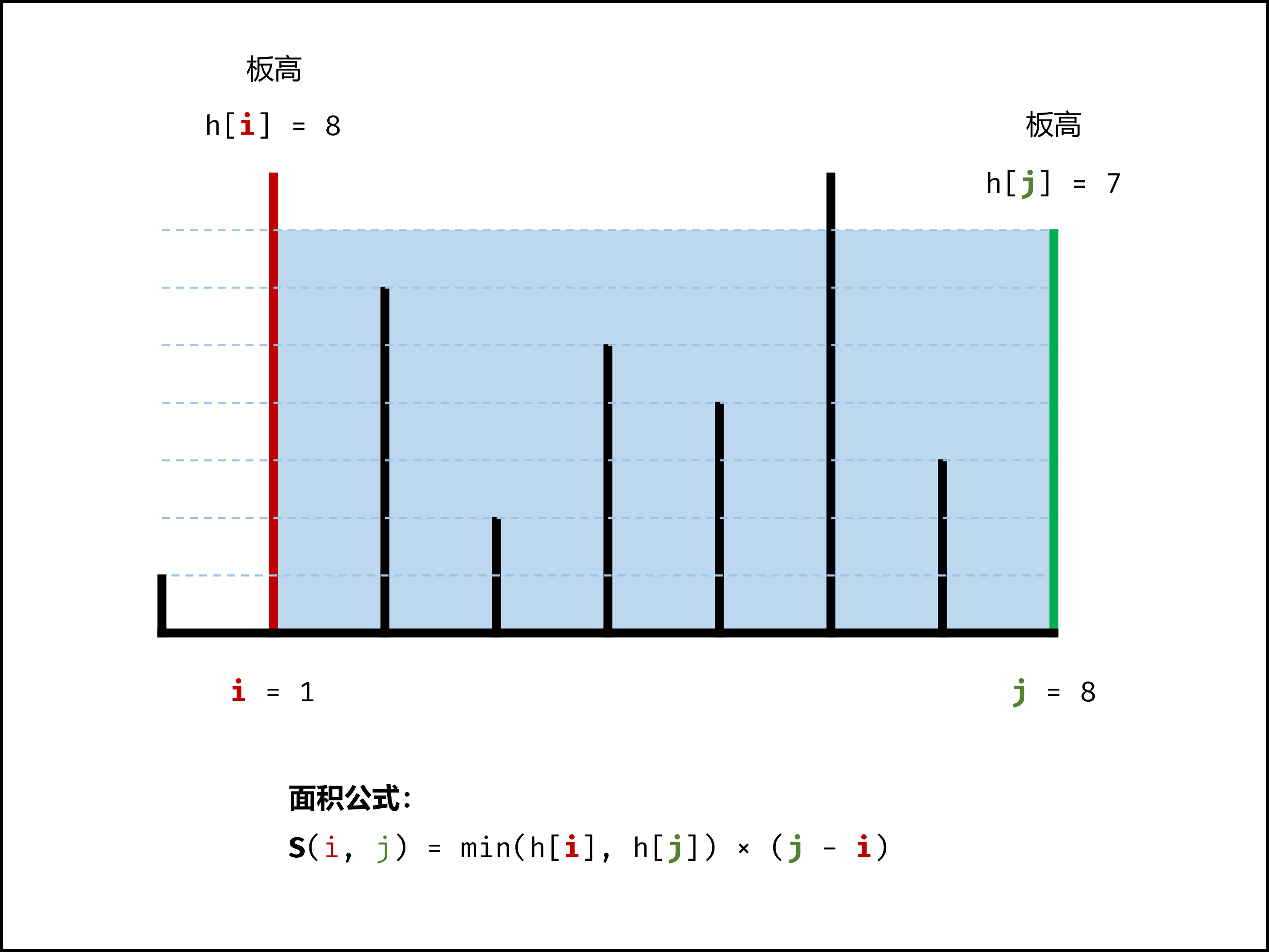
双指针左右夹逼,保留高个,移动低个。
-
一刷
-
二刷
-
三刷
-
四刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2018-07-13
*/
public static int maxArea(int[] height) {
int result = 0;
int left = 0, right = height.length - 1;
while (left < right) {
int area = Math.min(height[left], height[right]) * (right - left);
result = Math.max(result, area);
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2024-08-15 19:54:27
*/
public static int maxArea(int[] height) {
int left = 0, right = height.length - 1;
int result = 0;
while (left < right) {
if (height[left] < height[right]) {
result = Math.max(result, height[left] * (right - left));
left++;
} else {
result = Math.max(result, height[right] * (right - left));
right--;
}
}
return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2024-09-16 19:38:05
*/
public int maxArea(int[] height) {
int result = 0;
int left = 0, right = height.length - 1;
while (left < right) {
result = Math.max(result,
Math.min(height[left], height[right]) * (right - left));
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-20 18:13:51
*/
public int maxArea(int[] height) {
int result = 0;
int left = 0, right = height.length - 1;
while (left < right) {
int hi = Math.min(height[left], height[right]);
result = Math.max(result, hi * (right - left));
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return result;
}

