友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
Backtracking 回溯
首先介绍“回溯”算法的应用。“回溯”算法也叫“回溯搜索”算法,主要用于在一个庞大的空间里搜索我们所需要的问题的解。我们每天使用的“搜索引擎”就是帮助我们在庞大的互联网上搜索我们需要的信息。“搜索”引擎的“搜索”和“回溯搜索”算法的“搜索”意思是一样的。
“回溯”指的是“状态重置”,可以理解为“回到过去”、“恢复现场”,是在编码的过程中,是为了节约空间而使用的一种技巧。而回溯其实是“深度优先遍历”特有的一种现象。之所以是“深度优先遍历”,是因为我们要解决的问题通常是在一棵树上完成的,在这棵树上搜索需要的答案,一般使用深度优先遍历。
“全排列”就是一个非常经典的“回溯”算法的应用。我们知道,N 个数字的全排列一共有 N! 这么多个。
使用编程的方法得到全排列,就是在这样的一个树形结构中进行编程,具体来说,就是执行一次深度优先遍历,从树的根结点到叶子结点形成的路径就是一个全排列。
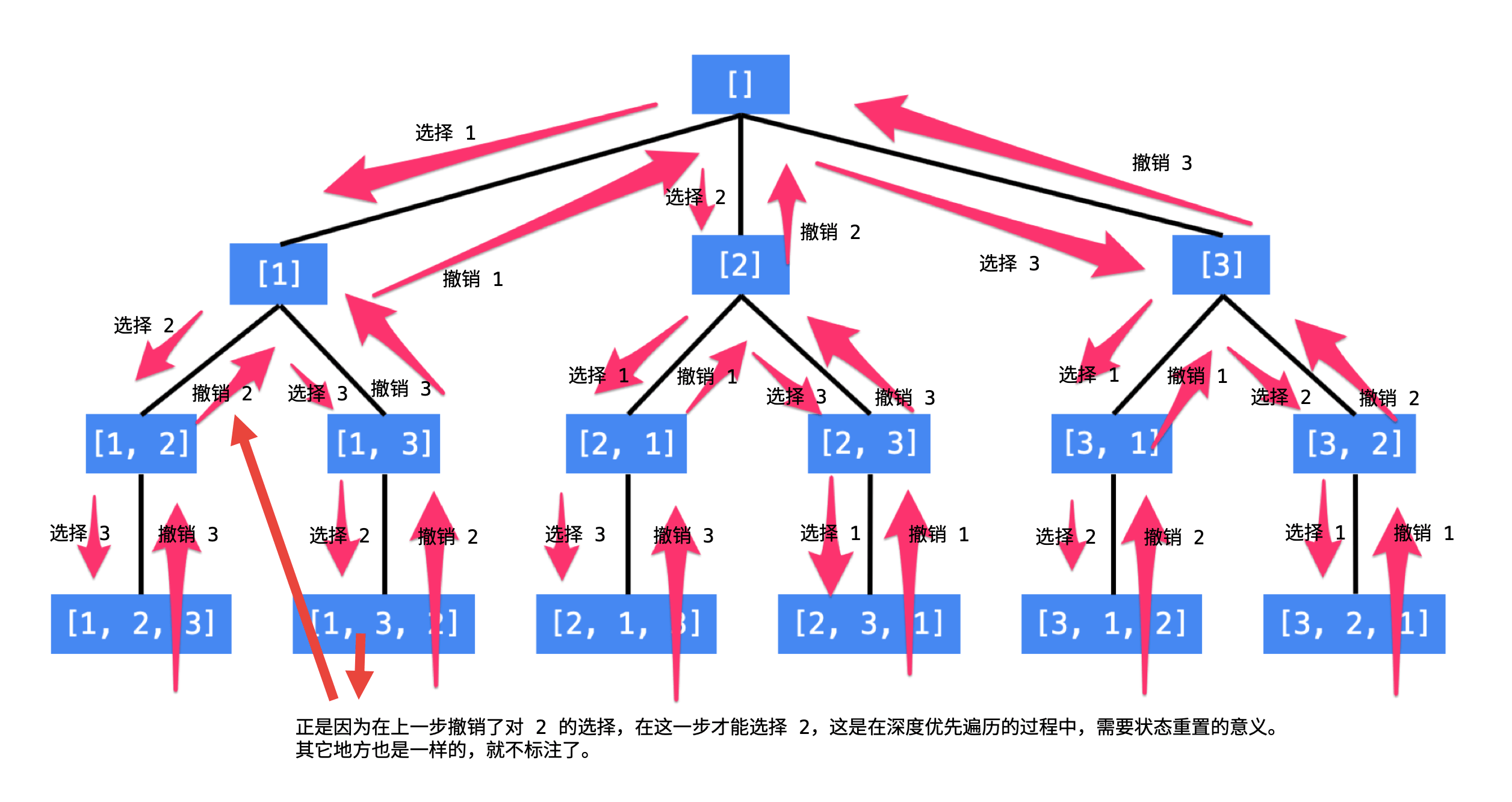
说明:
-
每一个结点表示了“全排列”问题求解的不同阶段,这些阶段通过变量的“不同的值”体现;
-
这些变量的不同的值,也称之为“状态”;
-
使用深度优先遍历有“回头”的过程,在“回头”以后,状态变量需要设置成为和先前一样;
-
因此在回到上一层结点的过程中,需要撤销上一次选择,这个操作也称之为“状态重置”;
-
深度优先遍历,可以直接借助系统栈空间,为我们保存所需要的状态变量,在编码中只需要注意遍历到相应的结点的时候,状态变量的值是正确的,具体的做法是:往下走一层的时候,
path变量在尾部追加,而往回走的时候,需要撤销上一次的选择,也是在尾部操作,因此path变量是一个栈。 -
深度优先遍历通过“回溯”操作,实现了全局使用一份状态变量的效果。
解决一个回溯问题,实际上就是一个决策树的遍历过程。只需要思考 3 个问题:
-
路径:也就是已经做出的选择。
-
选择列表:也就是你当前可以做的选择。
-
结束条件:也就是到达决策树底层,无法再做选择的条件。
代码方面,回溯算法的框架:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,特别简单。
必须说明的是,不管怎么优化,都符合回溯框架,而且时间复杂度都不可能低于 O(N!),因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点,不像动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
玩回溯,一定要画出递归调用树。
回溯优化,重要的是,要学会剪枝!
回溯三部曲:
-
定义递归函数以及参数
-
确定递归终止条件
-
思考递归单层搜索逻辑
经典题目
-
[1239-maximum-length-of-a-concatenated-string-with-unique-characters]
-
[1415-the-k-th-lexicographical-string-of-all-happy-strings-of-length-n]
-
[1467-probability-of-a-two-boxes-having-the-same-number-of-distinct-balls]
-
[1593-split-a-string-into-the-max-number-of-unique-substrings]
-
[1718-construct-the-lexicographically-largest-valid-sequence]
-
[1849-splitting-a-string-into-descending-consecutive-values]
-
[2002-maximum-product-of-the-length-of-two-palindromic-subsequences]
参考资料
-
698. 划分为k个相等的子集 - 经典回溯算法:集合划分问题「重要更新 🔥🔥🔥」 — 逐步优化的过程挺好的。

