LeetCode: 437. 路径总和 III

友情支持

如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜

支付宝

有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。

wx jikerizhi

公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。

437. 路径总和 III

LeetCode - 437. 路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

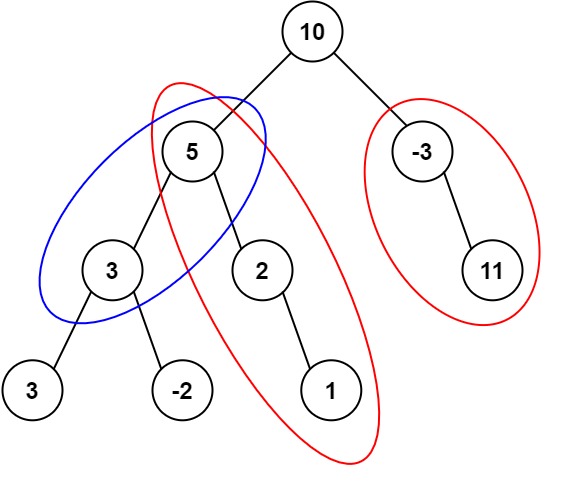
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-10⁹ <= Node.val <= 10⁹
-1000 <= targetSum <= 1000

思路分析

前缀和解法

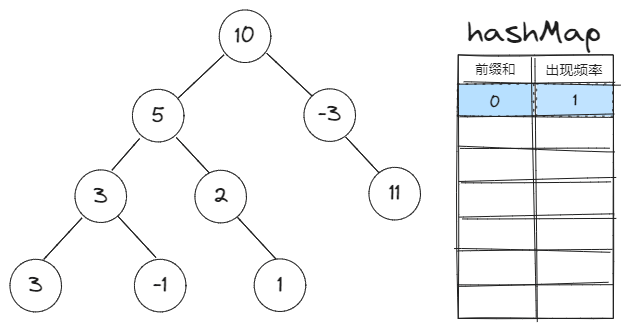
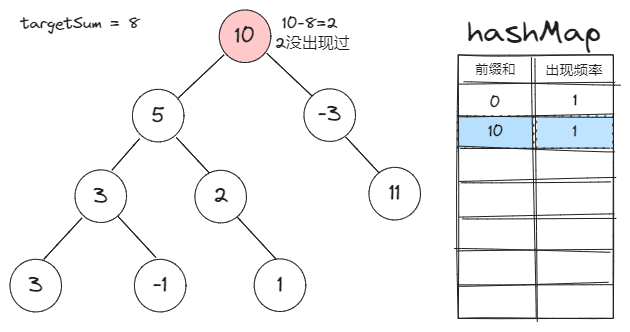
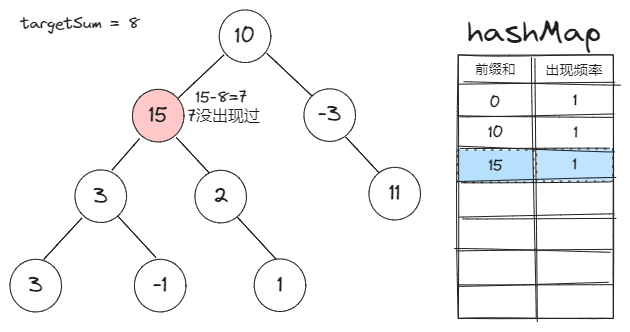
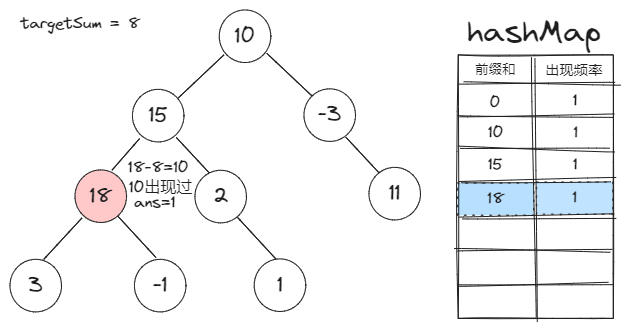
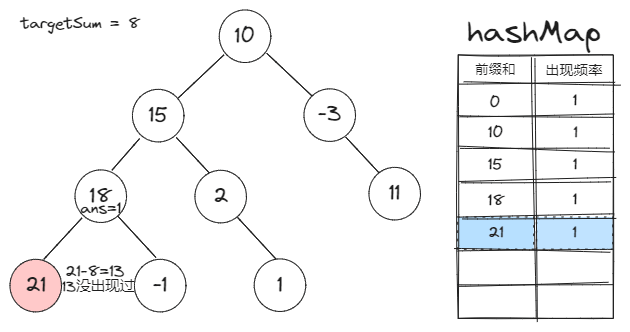
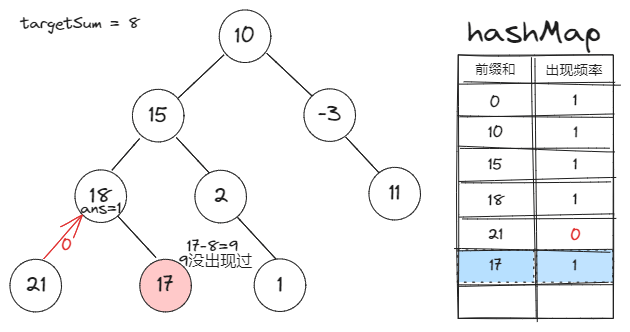
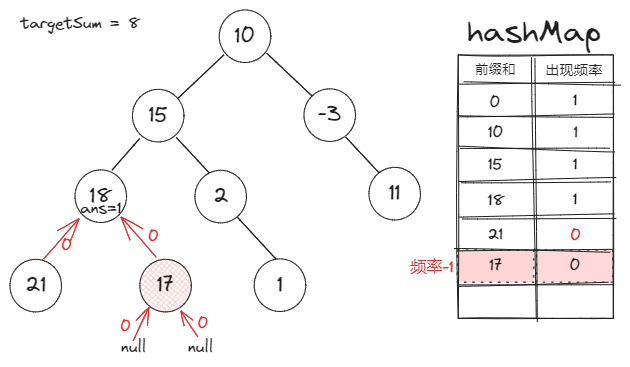
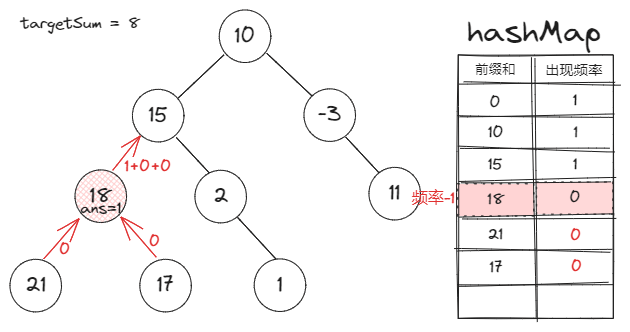
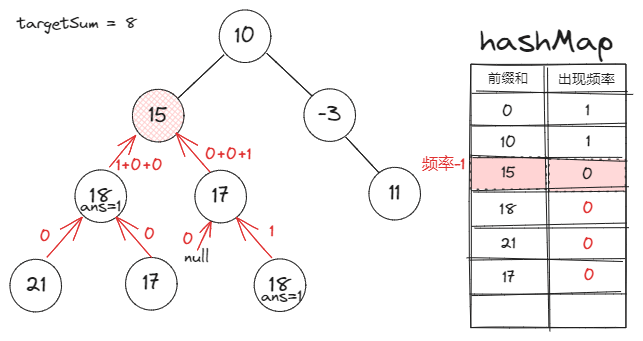
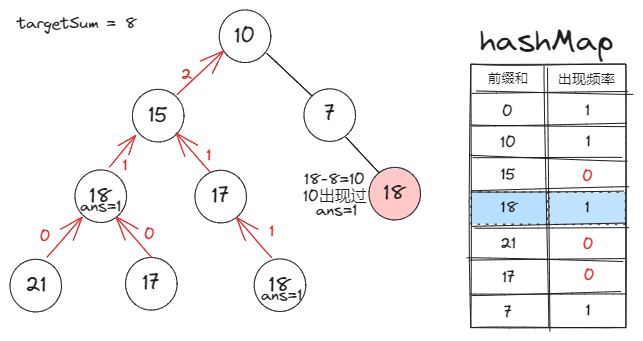
前缀和定义：一个节点的前缀和就是该节点到根之间的路径和。
前缀和对于本题的作用：两节点间的路径和=两节点的前缀和之差
Map 存的是什么: Map 的 key 是前缀和， value 是该前缀和在已遍历的节点中的出现频率
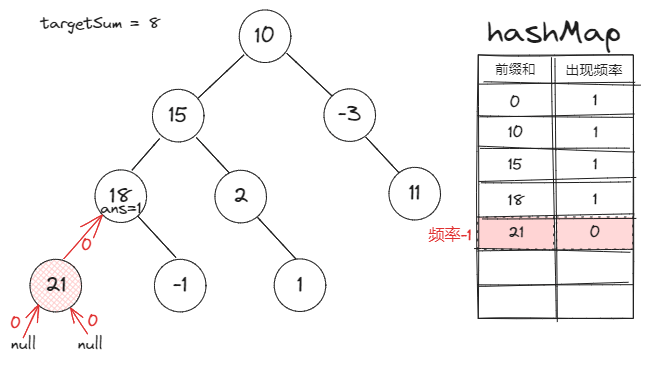
恢复状态的意义：
1. 题目要求：路径方向必须是向下的（只能从父节点到子节点）
2. 所以当我们讨论两个节点的前缀和差值时，有一个前提：一个节点必须是另一个节点的祖先节点。
3. 也就是说，当我们把一个节点的前缀和信息更新到 Map 里时，它应当只对其子节点有效。
4. 所以我们应该：在遍历完一个节点的所有子节点后，将其从 Map 中减去它的频率。

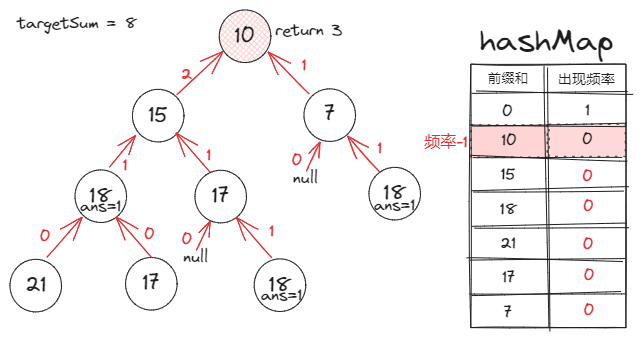
加一个 <0, 1> 的占位符，可以让代码写得更简洁。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Runtime: 23 ms, faster than 10.40% of Java online submissions for Path Sum III.
 * Memory Usage: 39.1 MB, less than 90.91% of Java online submissions for Path Sum III.
 *
 * Copy from: https://leetcode-cn.com/problems/path-sum-iii/solution/leetcode-437-path-sum-iii-by-li-xin-lei/[LeetCode 437 Path Sum III - 路径总和 III - 力扣（LeetCode）]
 */
public int pathSum(TreeNode root, int sum) {
    if (Objects.isNull(root)) {
        return 0;
    }
    return pathSum(root.left, sum) + pathSum(root.right, sum) + childPathSum(root, sum);
}

private int childPathSum(TreeNode root, int sum) {
    if (Objects.isNull(root)) {
        return 0;
    }
    int result = 0;
    if (root.val == sum) {
        result++;
    }
    result += childPathSum(root.left, sum - root.val);
    result += childPathSum(root.right, sum - root.val);
    return result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
    /**
     * Runtime: 23 ms, faster than 10.40% of Java online submissions for Path Sum III.
     * Memory Usage: 39.1 MB, less than 90.91% of Java online submissions for Path Sum III.
     *
     * Copy from: https://leetcode-cn.com/problems/path-sum-iii/solution/leetcode-437-path-sum-iii-by-li-xin-lei/[LeetCode 437 Path Sum III - 路径总和 III - 力扣（LeetCode）]
     */
//    public int pathSum(TreeNode root, int sum) {
//      if (root == null) {
//        return 0;
//      }
//      int nextSum = sum - root.val;
//      if (nextSum == 0) {
//        return 1 + pathSum(root.left, sum) + pathSum(root.right, sum);
//      } else {
//        return pathSum(root.left, sum) + pathSum(root.left, nextSum) +
//          pathSum(root.right, sum) + pathSum(root.right, nextSum);
//      }
//    }
public int pathSum(TreeNode root, int sum) {
  int result = 0;
  if (root == null) {
    return result;
  }
  if (sum == root.val) {
    result++;
  }
  // TODO 哪里错误？
  result += pathSum(root.left, sum - root.val);
  result += pathSum(root.right, sum - root.val);
  result += pathSum(root.left, sum);
  result += pathSum(root.right, sum);
  return result;
}

//  public int pathSum(TreeNode root, long targetSum) {
//    if (root == null) {
//      return 0;
//    }
//
//    int ret = rootSum(root, targetSum);
//    ret += pathSum(root.left, targetSum);
//    ret += pathSum(root.right, targetSum);
//    return ret;
//  }
//
//  public int rootSum(TreeNode root, long targetSum) {
//    int ret = 0;
//    if (root == null) {return 0;}
//    int val = root.val;
//    if (val == targetSum) {
//      ret++;
//    }
//    ret += rootSum(root.left, targetSum - val);
//    ret += rootSum(root.right, targetSum - val);
//    return ret;
//  }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 */
public int pathSum(TreeNode root, long sum) {
  if (root == null) {
    return 0;
  }
  return rootSum(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
}

public int rootSum(TreeNode root, long sum) {
  int result = 0;
  if (root == null) {
    return result;
  }
  int val = root.val;
  if (sum == val) {
    result++;
  }
  result += rootSum(root.left, sum - val);
  result += rootSum(root.right, sum - val);
  return result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * = 参考
 *
 * . https://leetcode.cn/problems/path-sum-iii/solutions/596361/dui-qian-zhui-he-jie-fa-de-yi-dian-jie-s-dey6/[437. 路径总和 III / 对前缀和解法的一点解释^]
 * . https://leetcode.cn/problems/path-sum-iii/solutions/100992/qian-zhui-he-di-gui-hui-su-by-shi-huo-de-xia-tian/[437. 路径总和 III / 前缀和，递归，回溯^]
 */
public int pathSum(TreeNode root, long target) {
  // key 是前缀和， value 是该前缀和的节点数量
  Map<Long, Integer> prefix = new HashMap<>();
  //前缀树为0的个数至少是一个
  prefix.put(0L, 1);
  // 前缀和的递归回溯思路
  return dfs(root, target, prefix, 0);
}

private int dfs(TreeNode root, long target, Map<Long, Integer> prefix, long sum) {
  // 1.递归终止条件
  if (root == null) {
    return 0;
  }

  // 2.本层要做的事情
  int result = 0;
  // 当前路径上的和
  sum += root.val;
  // TODO 这里不明白：
  //  从上往下，路径不应该只有一条吗？
  //  为什么是直接加 prefix.getOrDefault(sum - target, 0)？
  // 两节点间的路径和 = 两节点的前缀和之差
  // 得到我们想要前缀树的个数，想要前缀树值就是当前前缀树值减去目标值
  // target = prefixSum₂ - prefixSum₁
  result += prefix.getOrDefault(sum - target, 0);
  //将当前前缀树的值保存
  prefix.put(sum, prefix.getOrDefault(sum, 0) + 1);

  // 3.进入下一层
  //遍历左边
  result += dfs(root.left, target, prefix, sum);
  //遍历右边
  result += dfs(root.right, target, prefix, sum);

  // 4.回到本层，恢复状态，去除当前节点的前缀和数量
  // 一个节点必须是另一个节点的祖先节点。
  // 换句话说，当我们把一个节点的前缀和信息更新到map里时，它应当只对其子节点们有效。
  // 所以，退出该分支时，要把该分支的信息清理掉。
  // 这不是回溯吗？
  prefix.put(sum, prefix.get(sum) - 1);

  //结果是当前节点前缀树的个数加上左边满足的个数加右边满足的个数
  return result;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-09-26 21:53:27
 */
int result = 0;

public int pathSum(TreeNode root, int targetSum) {
  Map<Long, Integer> numToCounter = new HashMap<>();
  backtrack(root, targetSum, 0L, numToCounter);
  return result;
}

private void backtrack(TreeNode root, int targetSum,
                       long prefix, Map<Long, Integer> numToCounter) {
  if (root == null) {
    return;
  }
  prefix += root.val;
  if (prefix == targetSum) {
    result++;
  }
  result += numToCounter.getOrDefault(prefix - targetSum, 0);
  Integer original = numToCounter.getOrDefault(prefix, 0);
  numToCounter.put(prefix, original + 1);
  backtrack(root.left, targetSum, prefix, numToCounter);
  backtrack(root.right, targetSum, prefix, numToCounter);
  numToCounter.put(prefix, original);
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-10-13 21:21:14
 */
public int pathSum(TreeNode root, int targetSum) {
  if (Objects.isNull(root)) {
    return 0;
  }
  Map<Long, Integer> counter = new HashMap<>();
  counter.put(0L, 1);
  int[] result = {0};
  backtrack(root, counter, targetSum, 0L, result);
  return result[0];
}

private void backtrack(TreeNode root, Map<Long, Integer> counter,
                       int target, long path, int[] result) {
  if (Objects.isNull(root)) {
    return;
  }
  path += root.val;
  result[0] += counter.getOrDefault(path - target, 0);
  Integer origin = counter.getOrDefault(path, 0);
  counter.put(path, origin + 1);
  backtrack(root.left, counter, target, path, result);
  backtrack(root.right, counter, target, path, result);
  counter.put(path, origin);
}

思考题

感觉目前的解法还是有些繁琐。效仿 java解法时间100% 空间93% - 路径总和 III，设计一个更加高效的实现。

LeetCode: 437. 路径总和 III

友情支持

437. 路径总和 III

思路分析

前缀和解法

思考题

参考资料