友情支持
如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜
|
|
有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。
公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
1349. 参加考试的最大学生数
给你一个 m * n 的矩阵 seats 表示教室中的座位分布。如果座位是坏的（不可用），就用 # 表示；否则，用 . 表示。
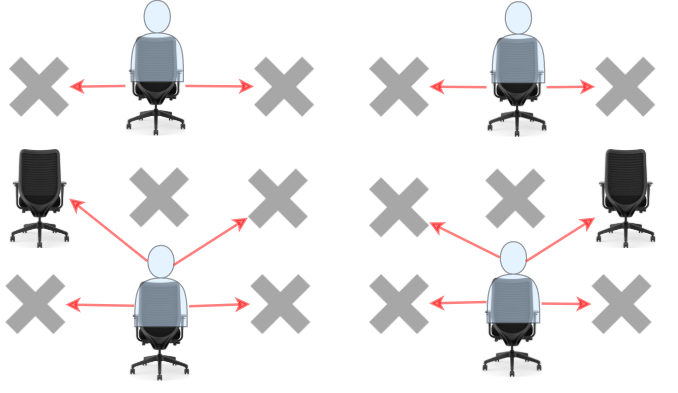
学生可以看到左侧、右侧、左上、右上这四个方向上紧邻他的学生的答卷，但是看不到直接坐在他前面或者后面的学生的答卷。请你计算并返回该考场可以容纳的同时参加考试且无法作弊的 最大 学生人数。
学生必须坐在状况良好的座位上。
示例 1：
输入：seats = [["#",".","#","#",".","#"],
[".","#","#","#","#","."],
["#",".","#","#",".","#"]]
输出：4
解释：教师可以让 4 个学生坐在可用的座位上，这样他们就无法在考试中作弊。
示例 2：
输入：seats = [[".","#"],
["#","#"],
["#","."],
["#","#"],
[".","#"]]
输出：3
解释：让所有学生坐在可用的座位上。
示例 3：
输入：seats = [["#",".",".",".","#"],
[".","#",".","#","."],
[".",".","#",".","."],
[".","#",".","#","."],
["#",".",".",".","#"]]
输出：10
解释：让学生坐在第 1、3 和 5 列的可用座位上。
提示：
-
seats只包含字符.和# -
m == seats.length -
n == seats[i].length -
1 <= m <= 8 -
1 <= n <= 8
思路分析
-
一刷（回溯，超时）
-
一刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/**
* 通过 50 / 57 个测试用例，后超时。
*
* @author D瓜哥 · https://www.diguage.com
* @since 2025-05-15 20:31:46
*/
int result = Integer.MIN_VALUE;
public int maxStudents(char[][] seats) {
int seatNo = seats.length * seats[0].length - 1;
backtrack(seats, seatNo, 0);
return result;
}
private void backtrack(char[][] seats, int seatNo, int num) {
if (seatNo < 0) {
result = Math.max(result, num);
return;
}
int row = seatNo / seats[0].length;
int column = seatNo % seats[0].length;
if (seats[row][column] == '.') {
for (int i = 1; i >= 0; i--) {
if (i == 0) {
seats[row][column] = '0';
backtrack(seats, seatNo - 1, num);
seats[row][column] = '.';
} else {
seats[row][column] = '1';
// 左
boolean left = false;
if (column > 0 && seats[row][column - 1] == '.') {
left = true;
seats[row][column - 1] = '0';
}
// 左上
boolean leftUp = false;
if (row > 0 && column > 0
&& seats[row - 1][column - 1] == '.') {
leftUp = true;
seats[row - 1][column - 1] = '0';
}
// 右
boolean right = false;
if (column < seats[0].length - 1 && seats[row][column + 1] == '.') {
right = true;
seats[row][column + 1] = '0';
}
// 右上
boolean rightUp = false;
if (row > 0 && column < seats[row].length - 1
&& seats[row - 1][column + 1] == '.') {
rightUp = true;
seats[row - 1][column + 1] = '0';
}
backtrack(seats, seatNo - 1, num + 1);
// 右上
if (rightUp) {
seats[row - 1][column + 1] = '.';
}
// 右
if (right) {
seats[row][column + 1] = '.';
}
// 左上
if (leftUp) {
seats[row - 1][column - 1] = '.';
}
// 左
if (left) {
seats[row][column - 1] = '.';
}
seats[row][column] = '.';
}
}
} else {
backtrack(seats, seatNo - 1, num);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-05-15 20:31:46
*/
public int maxStudents(char[][] seats) {
int m = seats.length;
int n = seats[0].length;
int[] a = new int[m]; // a[i] 是第 i 排可用椅子的下标集合
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (seats[i][j] == '.') {
a[i] |= 1 << j;
}
}
}
int[][] f = new int[m][1 << n];
for (int j = 1; j < (1 << n); j++) {
int lb = j & -j;
f[0][j] = f[0][j & ~(lb * 3)] + 1;
}
for (int i = 1; i < m; i++) {
for (int j = a[i]; j > 0; j = (j - 1) & a[i]) { // 枚举 a[i] 的子集 j
f[i][j] = f[i - 1][a[i - 1]]; // 第 i 排空着
for (int s = j; s > 0; s = (s - 1) & j) { // 枚举 j 的子集 s
if ((s & (s >> 1)) == 0) {// s 没有连续的 1
int t = a[i - 1] & ~(s << 1 | s >> 1); // 去掉不能坐人的位置
f[i][j] = Math.max(f[i][j], f[i - 1][t] + f[0][s]);
}
}
}
f[i][0] = f[i - 1][a[i - 1]];
}
return f[m - 1][a[m - 1]];
}