LeetCode: 60. Permutation Sequence

友情支持

如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜

支付宝

有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。

wx jikerizhi

公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。

60. Permutation Sequence

LeetCode - Permutation Sequence

The set [1,2,3,…,n] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order, we get the following sequence for n = 3:

"123"
"132"
"213"
"231"
"312"
"321"

Given n and k, return the k^th permutation sequence.

Note:

Given n will be between 1 and 9 inclusive.
Given k will be between 1 and n! inclusive.

Example 1:

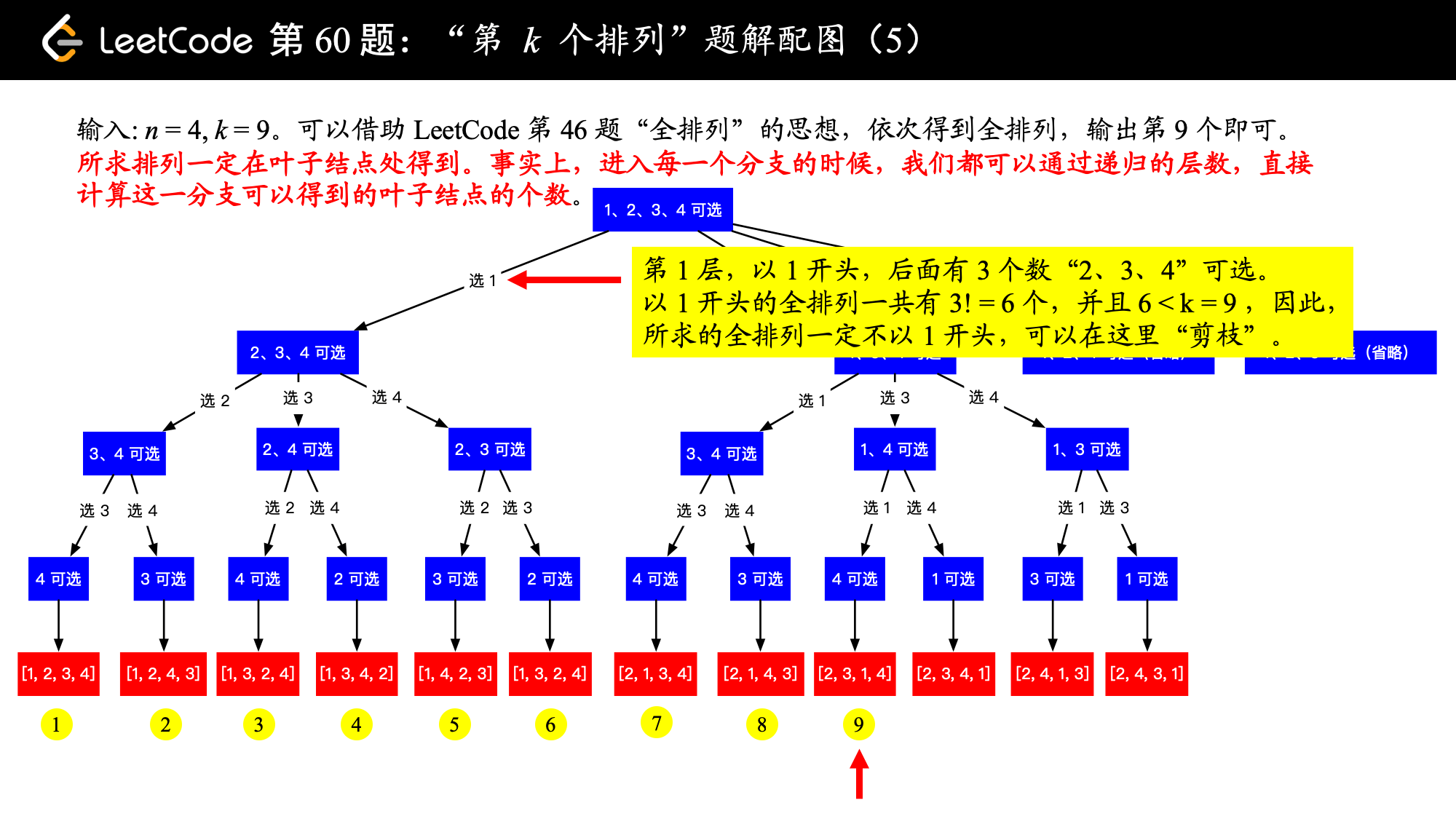
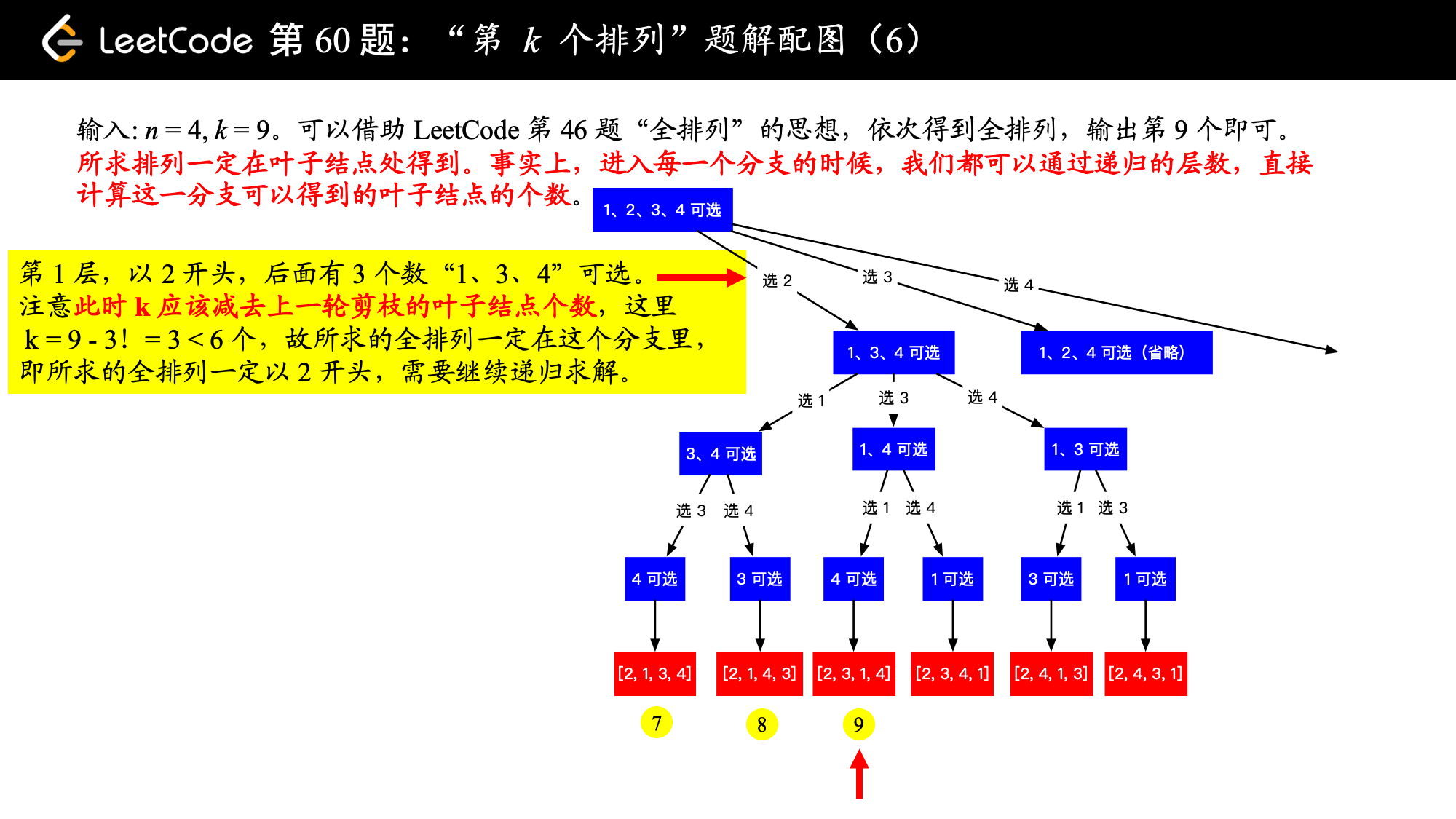
Input: n = 3, k = 3
Output: "213"

Example 2:

Input: n = 4, k = 9
Output: "2314"

解题分析

不需要生成所有的全排列。如图，通过剪枝，只需要生成需要的排列的路径即可。

这里的重点是如何剪枝！

思考题

对回溯再推敲推敲！

参考资料

深度优先遍历 + 剪枝、双链表模拟 - 第k个排列 - 力扣（LeetCode）

The set [1,2,3,…,n] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order, we get the following sequence for n = 3:

"123"
"132"
"213"
"231"
"312"
"321"

Given n and k, return the k^th permutation sequence.

Note:

Given n will be between 1 and 9 inclusive.
Given k will be between 1 and n! inclusive.

Example 1:

Input: n = 3, k = 3
Output: "213"

Example 2:

Input: n = 4, k = 9
Output: "2314"

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/**
 * Runtime: 1 ms, faster than 99.26% of Java online submissions for Permutation Sequence.
 * Memory Usage: 37.2 MB, less than 20.83% of Java online submissions for Permutation Sequence.
 *
 * Copy from: https://leetcode-cn.com/problems/permutation-sequence/solution/hui-su-jian-zhi-python-dai-ma-java-dai-ma-by-liwei/[深度优先遍历 + 剪枝、双链表模拟 - 第k个排列 - 力扣（LeetCode）]
 */
private boolean[] used;
private int[] factorial;
private int n;
private int k;
private List<Integer> path;
public String getPermutation(int n, int k) {
    this.n = n;
    this.k = k;
    used = new boolean[n + 1];
    factorial = new int[n + 1];
    factorial[0] = 1;
    for (int i = 1; i <= n; i++) {
        factorial[i] = factorial[i - 1] * i;
    }
    path = new ArrayList<>();
    dfs(0);
    StringBuilder builder = new StringBuilder();
    for (Integer integer : path) {
        builder.append(integer);
    }
    return builder.toString();
}

private void dfs(int index) {
    if (index == n) {
        return;
    }
    int cnt = factorial[n - 1 - index];
    for (int i = 1; i <= n; i++) {
        if (used[i]) {
            continue;
        }
        if (cnt < k) {
            k -= cnt;
            continue;
        }
        path.add(i);
        used[i] = true;
        dfs(index + 1);
    }
}

/**
 * Time Limit Exceeded
 */
public String getPermutationRecursion(int n, int k) {
    List<Integer> nums = new ArrayList<>(n);
    for (int i = 1; i <= n; i++) {
        nums.add(i);
    }
    List<String> permutations = new LinkedList<>();
    permutations(nums, 0, permutations);
    ArrayList<String> sp = new ArrayList<>(permutations);
    sp.sort(Comparator.naturalOrder());
    return sp.get(k - 1);
}

private void permutations(List<Integer> nums, int index, List<String> result) {
    if (index == nums.size()) {
        StringBuilder builder = new StringBuilder(index);
        for (int num : nums) {
            builder.append(num);
        }
        result.add(builder.toString());
        return;
    }
    for (int i = index; i < nums.size(); i++) {
        Collections.swap(nums, i, index);
        permutations(nums, index + 1, result);
        Collections.swap(nums, i, index);
    }
}