友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
199. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
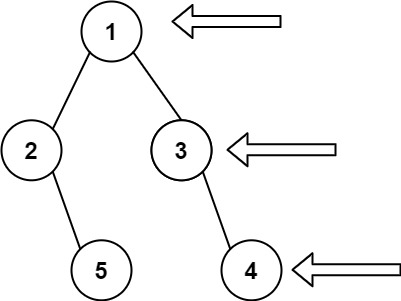
输入: [1,2,3,null,5,null,4] 输出: [1,3,4] 解释: 1 <--- / \ 2 3 <--- \ \ 5 4 <---
示例 2:
输入: [1,null,3] 输出: [1,3]
示例 3:
输入: [] 输出: []
提示:
-
二叉树的节点个数的范围是
[0, 100] -
-100 <= Node.val <= 100
思路分析
最简单的思路就是利用 BFS 思想进行分层遍历,然后每层取最后一个节点的值。
深度优先遍历,按照 <level, node> 的格式,把每个节点都放到 Map 里,因为是先左后右,所以,每层最后只剩下了最右边的元素。
其实,可以不用 Map,直接用 List 即可。不过,要注意先根遍历和中根遍历的区别:先根遍历每层都是按顺序从上到下添加到 List;而中根遍历,每次都是最下层到,所以,要添加 null 占位符把 List 给撑起来,后续直接按照坐标设置。
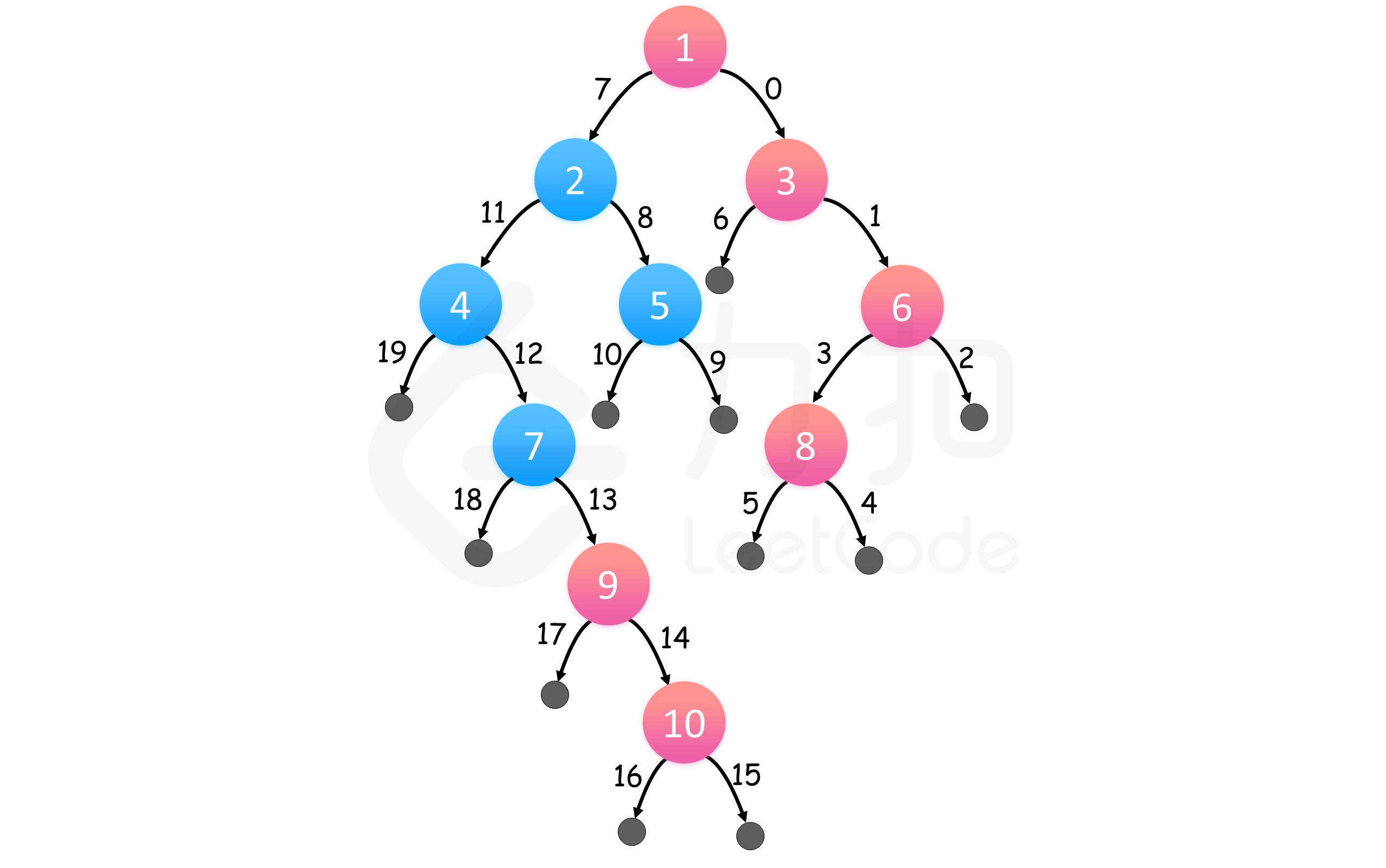
另外,仔细体会一下“左中右遍历”和“右中左遍历”的区别。
右中左深度优先遍历
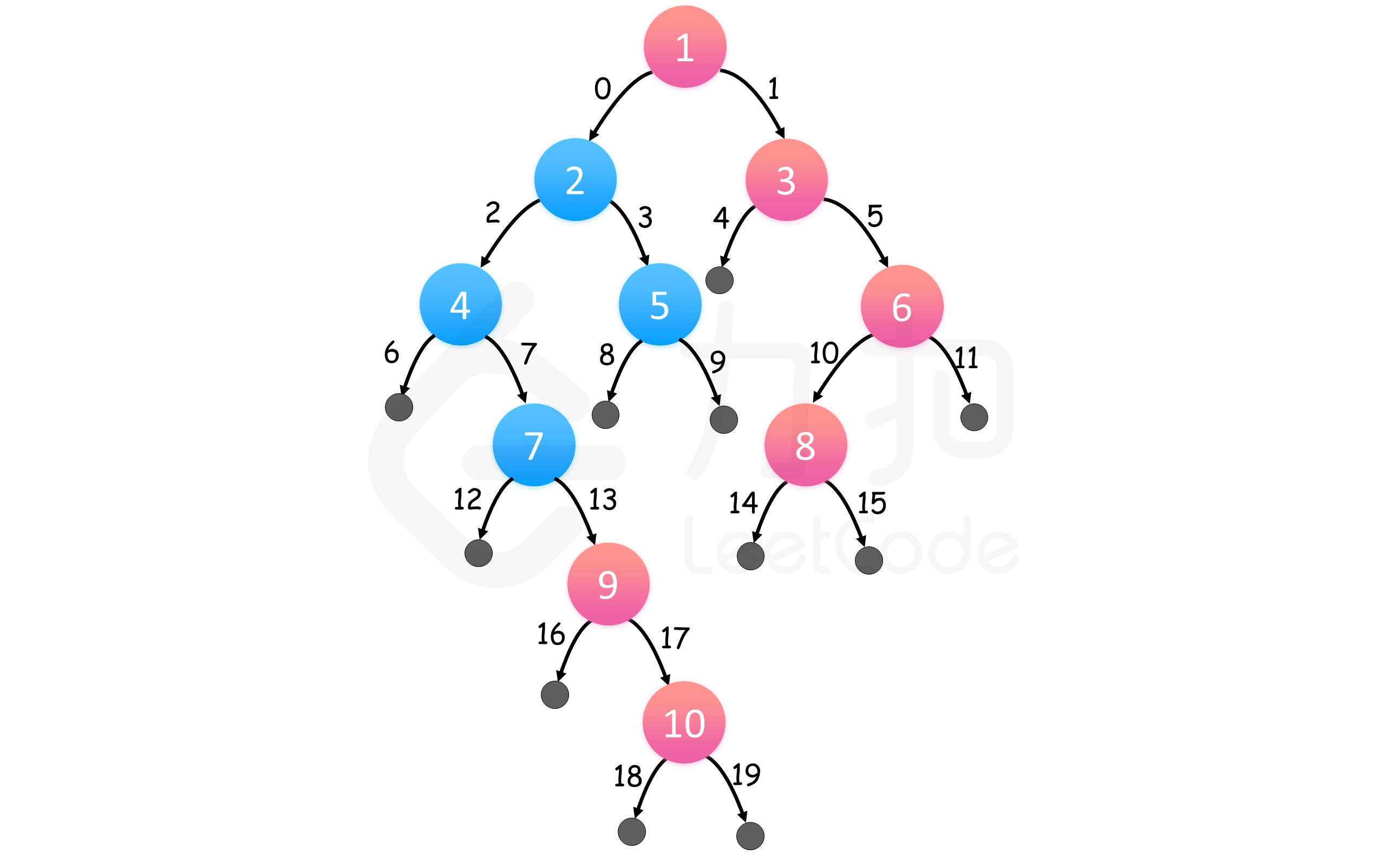
广度优先遍历
-
一刷
-
一刷(深度优先)
-
二刷
-
三刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2024-06-25 11:30:36
*/
public List<Integer> rightSideView(TreeNode root) {
if (root == null) {
return Collections.emptyList();
}
List<Integer> result = new ArrayList<>();
Deque<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
if (i == size - 1) {
result.add(node.val);
}
}
}
return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
* 参考 https://leetcode.cn/problems/binary-tree-right-side-view/solutions/2015061/ru-he-ling-huo-yun-yong-di-gui-lai-kan-s-r1nc/[199. 二叉树的右视图 - 【视频】如何灵活运用递归?^]
*
* @author D瓜哥 · https://www.diguage.com
* @since 2024-06-25 14:44:16
*/
public List<Integer> rightSideView(TreeNode root) {
List<Integer> result = new ArrayList<>();
dfs(root, 0, result);
return result;
}
private void dfs(TreeNode root, int level, List<Integer> result) {
if (root == null) {
return;
}
// 这个深度首次遇到
if (level == result.size()) {
result.add(root.val);
}
// 先递归右子树,保证首次遇到的一定是最右边的节点
dfs(root.right, level + 1, result);
dfs(root.left, level + 1, result);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-05-04 21:45:49
*/
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> levelToNode = new HashMap<>();
dfs(root, 0, levelToNode);
return new ArrayList<>(levelToNode.values());
}
private void dfs(TreeNode root, int level, Map<Integer, Integer> levelToNode) {
if (root == null) {
return;
}
levelToNode.put(level, root.val);
dfs(root.left, level + 1, levelToNode);
dfs(root.right, level + 1, levelToNode);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-10-25 10:51:00
*/
public List<Integer> rightSideView(TreeNode root) {
List<Integer> result = new ArrayList<>();
dfs(root, result, 0);
return result;
}
private void dfs(TreeNode root, List<Integer> result, int level) {
if (null == root) {
return;
}
// 如果是先根遍历,每层都会根节点先到,
// 直接在 List 里面追加(add)即可
if (level == result.size()) {
result.add(root.val);
} else {
// 如果是左中右遍历,左中节点先到,那么就需要更新
// 如果是右中左遍历,右节点先到,直接添加就无需更新
result.set(level, root.val);
}
dfs(root.left, result, level + 1);
// 如果是中根遍历,会先遍历到最深的叶子节点,
// 所以需要用 null 占位符把 List 给撑起来
// while (result.size() <= level) {
// result.add(null);
// }
// result.set(level, root.val);
dfs(root.right, result, level + 1);
}
这道题是 102. 二叉树的层序遍历 的延伸。
参考资料
-
199. 二叉树的右视图 - 官方题解 — 感觉官方的深度优先搜索的解法不对,或者实际是广度优先。

