友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
337. 打家劫舍 III
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额_ 。
示例 1:
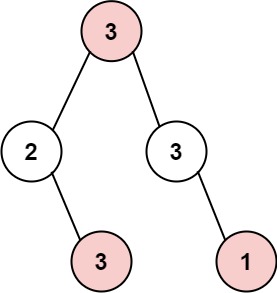
输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
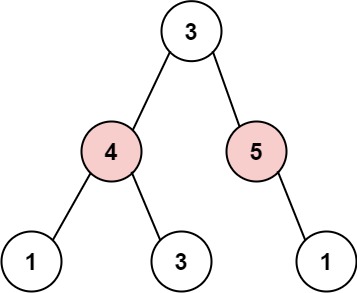
输入: root = [3,4,5,1,3,null,1] 输出: 9 解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
提示:
-
树的节点数在
[1, 104]范围内 -
0 <= Node.val <= 104
思路分析
由于题目给出示例的误导,这里存在一个误区:在不选父节点时,子树选最优解不受任何干扰,也就是说子树的跟节点可选也可以不选。所以,可以将这个问题简化为,分选根节点和不选根节点,两种情况考虑:
-
选父节点,则子树必定不能选根节点;
-
如果不选跟节点,则子树可以在选根节点和不选跟节点中选最优解就好。
然后在这上面两种情况中选出最优解。
-
一刷
-
二刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
* Runtime: 0 ms, faster than 100.00% of Java online submissions for House Robber III.
* Memory Usage: 41.3 MB, less than 13.89% of Java online submissions for House Robber III.
*
* Copy from: https://leetcode-cn.com/problems/house-robber-iii/solution/java-2ms-by-horanol/[java 2ms - 打家劫舍 III - 力扣(LeetCode)]
*
* @author D瓜哥 · https://www.diguage.com
* @since 2020-01-29 16:34
*/
public int rob(TreeNode root) {
int[] robs = doRob(root);
return Math.max(robs[0], robs[1]);
}
public int[] doRob(TreeNode root) {
int[] result = new int[2];
if (Objects.isNull(root)) {
return result;
}
int[] left = doRob(root.left);
int[] right = doRob(root.right);
result[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
result[1] = left[0] + right[0] + root.val;
return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-17 15:26:16
*/
public int rob(TreeNode root) {
if (root == null) return 0;
int[] dp = dfs(root);
return Math.max(dp[0], dp[1]);
}
private int[] dfs(TreeNode root) {
if (root == null) {
return new int[]{0, 0};
}
// result[0] 表示包含当前根节点时,可取的最大值
// result[1] 表示不包含当前根节点,也就是下级节点可取的最大值
// dp[0] = max(root.val + left[1] + right[1], left[0] + right[0])
// 在取当前节点和不取当前节点两者中选最大的一个
// 向上推进一层,则下一级的 result[0] 之和,就是上一层的 result[1]
int[] left = dfs(root.left);
int[] right = dfs(root.right);
int currMax = Math.max(root.val + left[1] + right[1], left[0] + right[0]);
int childMax = left[0] + right[0];
return new int[]{currMax, childMax};
}
参考资料
-
337. 打家劫舍 III - 三种方法解决树形动态规划问题-从入门级代码到高效树形动态规划代码实现 — 从暴力递归,到备忘录,到最优方案,层层推进。

