友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
52. N 皇后 II
n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1:
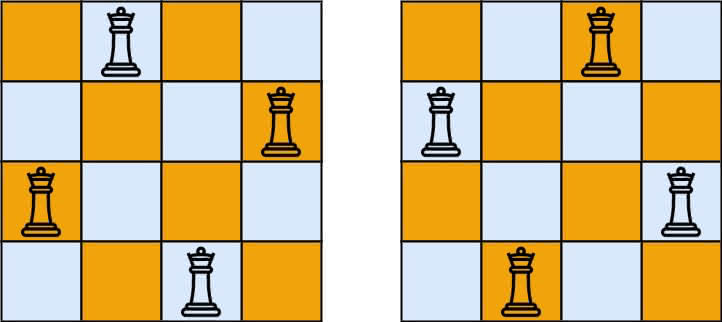
输入:n = 4 输出:2 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:1
提示:
-
1 <= n <= 9
思路分析
解题分析参考 51. N-Queens。
新建一个棋盘,将皇后放在棋盘上,每次放置前判断是否能放置,如果可以放置,则放置,然后从下一行第一个位置继续下去。直到结束。
| 看题解,不需要构建棋盘也可以模拟下棋过程。 |
-
一刷
-
二刷
-
三刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
* Runtime: 1 ms, faster than 95.68% of Java online submissions for N-Queens II.
* Memory Usage: 36 MB, less than 8.70% of Java online submissions for N-Queens II.
*
* @author D瓜哥 · https://www.diguage.com
* @since 2020-02-05 16:25
*/
private int result = 0;
public int totalNQueens(int n) {
int[][] matrix = new int[n][n];
backtrack(matrix, 0, 0);
return result;
}
private void backtrack(int[][] matrix, int y, int step) {
if (step == matrix.length) {
result++;
return;
}
for (int xi = 0; xi < matrix[0].length; xi++) {
if (isValid(matrix, y, xi)) {
matrix[y][xi] = 1;
backtrack(matrix, y + 1, step + 1);
matrix[y][xi] = 0;
}
}
}
private boolean isValid(int[][] matrix, int y, int x) {
int len = matrix.length;
// 同列
for (int i = 0; i < y; i++) {
if (matrix[i][x] == 1) {
return false;
}
}
// 左上角
for (int i = 1; i < len && y - i >= 0 && x - i >= 0; i++) {
if (matrix[y - i][x - i] == 1) {
return false;
}
}
// 右上角:从右上角到最下角的对角线,他们 "行号 + 列号 = 常数"
int sum = x + y;
for (int yi = y - 1; yi >= 0 && 0 <= sum - yi && sum - yi < len; yi--) {
if (matrix[yi][sum - yi] == 1) {
return false;
}
}
return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
* 自己实现
*
* @author D瓜哥 · https://www.diguage.com
* @since 2024-06-29 20:35:25
*/
private int result = 0;
public int totalNQueens(int n) {
int[][] matrix = new int[n][n];
backtrack(matrix, 0, 0);
return result;
}
private void backtrack(int[][] matrix, int step, int count) {
int size = matrix.length;
int pow = size * size;
printMatrix(matrix);
if (step > pow) {
return;
} else if (size == count) {
result++;
} else {
for (int i = step; i < pow; i++) {
int row = i / size;
int col = i % size;
if (isValid(matrix, row, col)) {
matrix[row][col] = 1;
backtrack(matrix, (row + 1) * size, count + 1);
matrix[row][col] = 0;
}
}
}
}
private boolean isValid(int[][] matrix, int row, int col) {
int length = matrix.length;
for (int i = 0; i < length; i++) {
if (matrix[row][i] == 1) {
return false;
}
if (i < row && matrix[i][col] == 1) {
return false;
}
}
for (int i = 0; i < length; i++) {
// 左上角
if (0 <= row - i && 0 <= col - i && matrix[row - i][col - i] == 1) {
return false;
}
// 右上角
if (0 <= row - i && col + i < length && matrix[row - i][col + i] == 1) {
return false;
}
}
return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2020-02-05 16:25
*/
public int totalNQueens(int n) {
boolean[][] board = new boolean[n][n];
return backtrack(board, 0, 0, 0);
}
private int backtrack(boolean[][] board, int row, int col, int cnt) {
int length = board.length;
if (row >= length && cnt == length) {
return 1;
}
int result = 0;
for (int r = row; r < length; r++) {
for (int c = col; c < length; c++) {
if (isValid(board, r, c)) {
board[r][c] = true;
result += backtrack(board, r + 1, 0, cnt + 1);
board[r][c] = false;
} else {
// 如果一行中都没有可以放置的,则不是正确解
if (c == length - 1) {
return result;
}
}
}
}
return result;
}
private boolean isValid(boolean[][] board, int row, int col) {
int length = board.length;
for (int i = 0; i < length; i++) {
if (board[row][i]) {
return false;
}
if (board[i][col]) {
return false;
}
if (row - i >= 0 && col - i >= 0 && board[row - i][col - i]) {
return false;
}
// 右下方对角线还没处理到,不需要判断
// if (row + i < length && col + i < length && board[row + i][col + i]) {
// return false;
// }
if (row - i >= 0 && col + i < length && board[row - i][col + i]) {
return false;
}
// 左下方对角线还没处理到,不需要判断
// if (row + i < length && col - i >= 0 && board[row + i][col - i]) {
// return false;
// }
}
return true;
}

