友情支持
如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜
|
|
有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。
公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
84. 柱状图中最大的矩形
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。
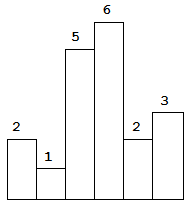
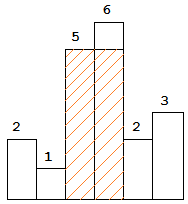
示例 1:
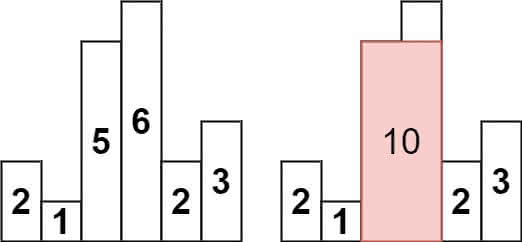
输入：heights = [2,1,5,6,2,3] 输出：10 解释：最大的矩形为图中红色区域，面积为 10
示例 2：
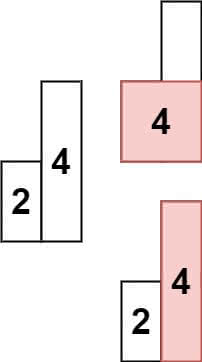
输入： heights = [2,4] 输出： 4
提示：
-
1 <= heights.length <=105 -
0 <= heights[i] <= 104
思路分析
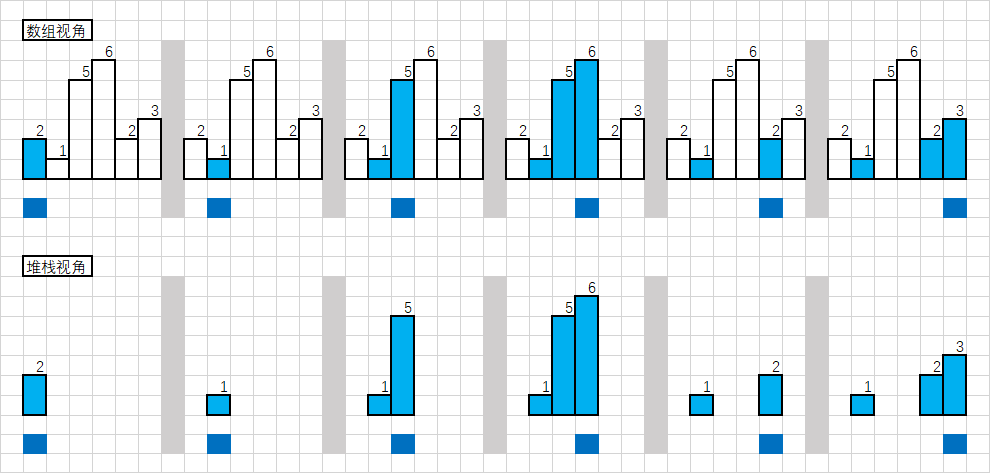
单调递增栈
当需要出栈的时候，就是当前元素小于栈顶元素。这样，弹出栈顶元素，以弹出的栈顶元素作为高，由于是单调递增栈，现在栈顶元素是小于已弹出的栈顶元素。所以，栈顶元素和当前坐标就是以弹出的栈顶元素的左右两个更低的柱子。那么，就弹出的栈顶元素作为高，当前坐标-栈顶元素（存的坐标）-1作为宽，就可以计算相关柱子组成的面积了。
哨兵技巧非常巧妙。即可减少栈的非空判断，又可以推进剩余元素的计算（如果没有最后的零点哨兵，栈里单调递增的元素最后还要单独处理。）
-
一刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-23 20:07:47
*/
public int largestRectangleArea(int[] heights) {
int length = heights.length;
if (length == 1) {
return heights[0];
}
int[] newHeights = new int[length + 2];
// 两端是两个哨兵
newHeights[0] = 0;
newHeights[length + 1] = 0;
System.arraycopy(heights, 0, newHeights, 1, length);
heights = newHeights;
int result = 0;
length += 2;
Deque<Integer> stack = new ArrayDeque<>();
stack.push(0); // 哨兵，可以省去栈的非空判断
for (int i = 1; i < length; i++) {
// 单调递增栈
// 当需要出栈的时候，就是当前元素小于栈顶元素。
// 这样，弹出栈顶元素，以弹出的栈顶元素作为高，
// 由于是单调递增栈，现在栈顶元素是小于已弹出的栈顶元素。
// 所以，栈顶元素和当前坐标就是以弹出的栈顶元素的左右两个更低的柱子
// 那么，就弹出的栈顶元素作为高，当前坐标-栈顶元素（存的坐标）-1作为宽
// 就可以计算相关柱子组成的面积了。
while (heights[i] < heights[stack.peekLast()]) {
int currHeight = heights[stack.pollLast()];
int currWidth = i - stack.peekLast() - 1;
result = Math.max(result, currHeight * currWidth);
}
stack.addLast(i);
}
return result;
}
参考资料
-
84. 柱状图中最大的矩形 - 暴力解法、栈（单调栈、哨兵技巧） — 哨兵技巧牛逼
-
84. 柱状图中最大的矩形 - 官方题解 — 看的稀里糊涂。