友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
72. 编辑距离
给你两个单词 word1 和 word2,请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
-
插入一个字符
-
删除一个字符
-
替换一个字符
示例1:
输入:word1 = "horse", word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
示例2:
输入:word1 = "intention", word2 = "execution" 输出:5 解释: intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')
提示:
-
0 <= word1.length, word2.length <= 500 -
word1和word2由小写英文字母组成
思路分析
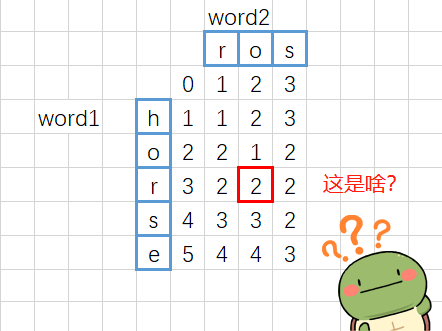
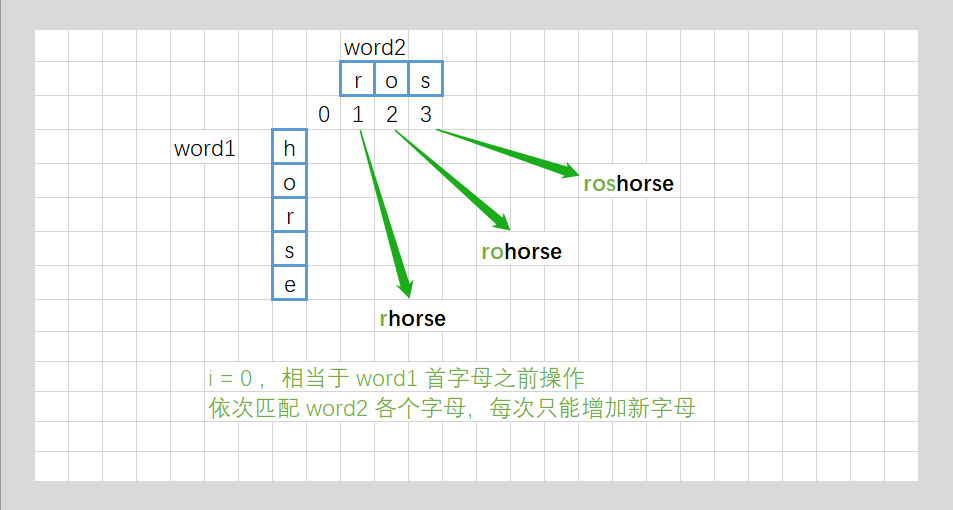
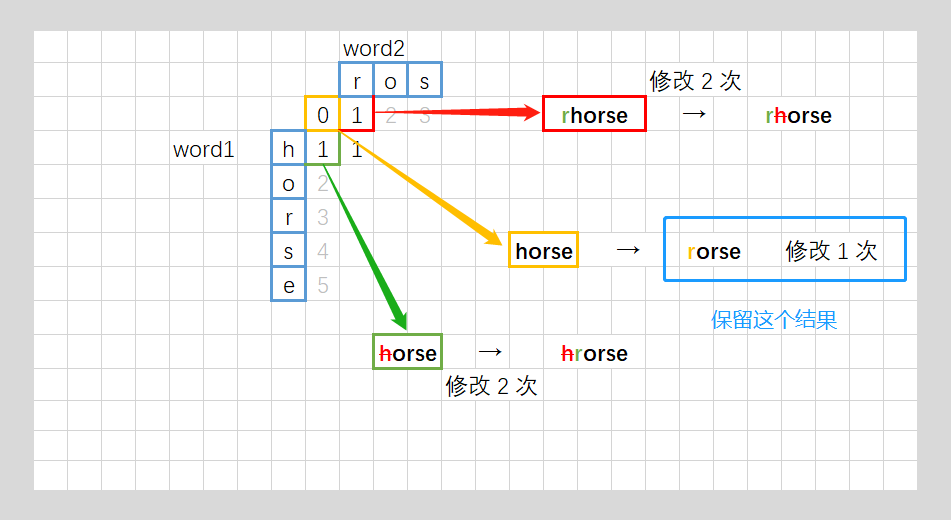
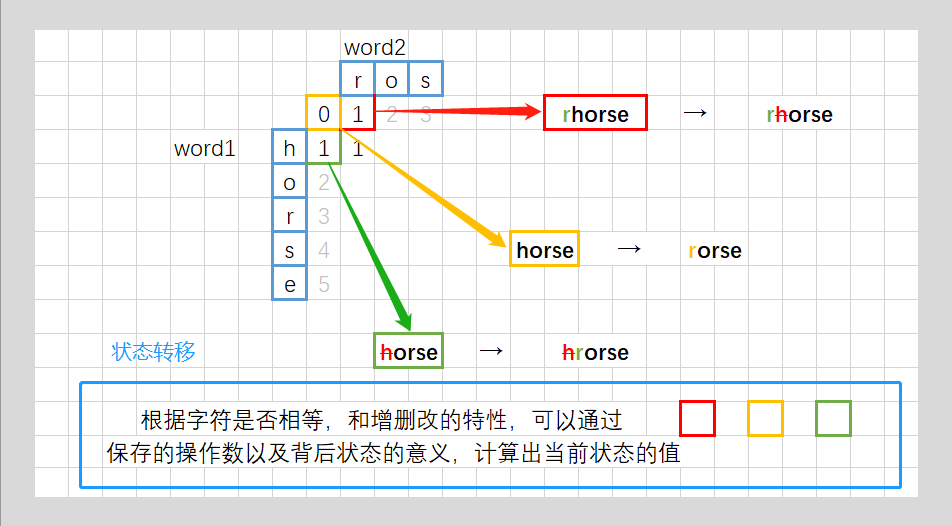
动态规划:计算 dp[c][r] 时,从相邻三个元素获取递推的含义还要好好思考一下,“增”、“删”和“改”的含义要理解清楚。
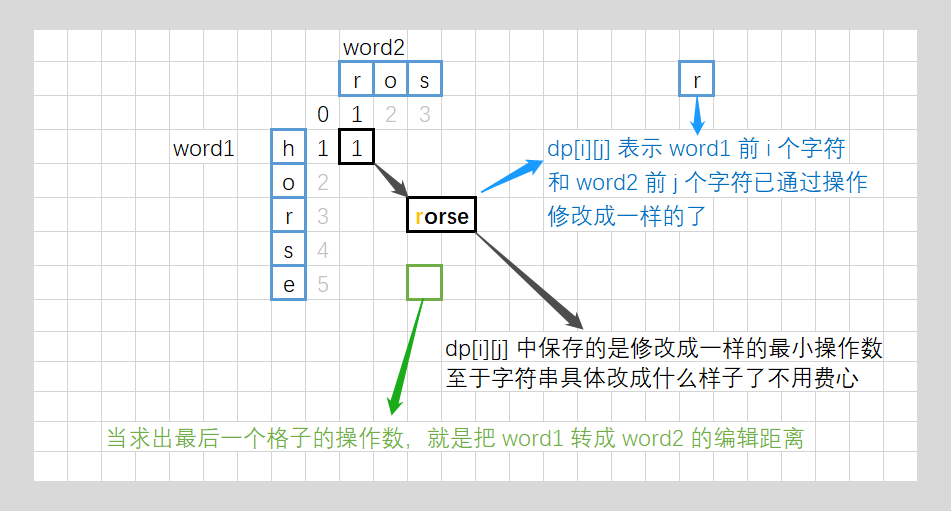
dp[i][j] 代表 word1 中前 i 个字符,变换到 word2 中前 j 个字符,最短需要操作的次数。


-
一刷
-
二刷
-
三刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2024-09-30 17:32:45
*/
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
// 1. 确定 dp[i][j] 含义
int[][] dp = new int[len1 + 1][len2 + 1];
// 3. 初始化基本状态
for (int i = 0; i <= len1; i++) {
dp[i][0] = i;
}
for (int i = 0; i <= len2; i++) {
dp[0][i] = i;
}
// 确定遍历过程
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
// 2. 确定转移方程
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
// 删除操作:dp[i - 1][j]
// 增加操作:dp[i][j - 1]
// 替换操作:dp[i - 1][j - 1]
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]),
dp[i - 1][j - 1]) + 1;
}
}
}
return dp[len1][len2];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-20 19:29:44
*/
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
dp[i][0] = i;
}
for (int i = 1; i <= n; i++) {
dp[0][i] = i;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
// 替换:dp[i][j] = dp[i-1][j-1] + 1
// 删除:dp[i][j] = dp[i-1][j] + 1
// 插入:dp[i][j] = dp[i][j-1] + 1
// dp[i][j] = min{dp[i-1][j-1], dp[i][j-1], dp[i-1][j]} + 1
int min = Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]);
dp[i][j] = min + 1;
}
}
}
return dp[m][n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-11-20 22:42:36
*/
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int r = 0; r <= n; r++) {
dp[0][r] = r;
}
// 可以把这步和下面的循环合并,减少一次循环
for (int c = 0; c <= m; c++) {
dp[c][0] = c;
}
for (int c = 1; c <= m; c++) {
for (int r = 1; r <= n; r++) {
if (word1.charAt(c - 1) == word2.charAt(r - 1)) {
dp[c][r] = dp[c - 1][r - 1];
} else {
int min = Math.min(dp[c][r - 1], dp[c - 1][r]);
min = Math.min(min, dp[c - 1][r - 1]);
dp[c][r] = min + 1;
}
}
}
return dp[m][n];
}
参考资料
-
72. 编辑距离 - 【视频】教你一步步思考动态规划,从记忆化搜索到递推到空间优化! — 从递归到动态规划,从矩阵到一维数组,逐步优化。

