友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
309. Best Time to Buy and Sell Stock with Cooldown
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
-
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
-
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Input: [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]解题分析
针对 一个方法团灭 6 道股票问题 - 最佳买卖股票时机含冷冻期 - 力扣(LeetCode) 这个解题框架,进行小试牛刀。
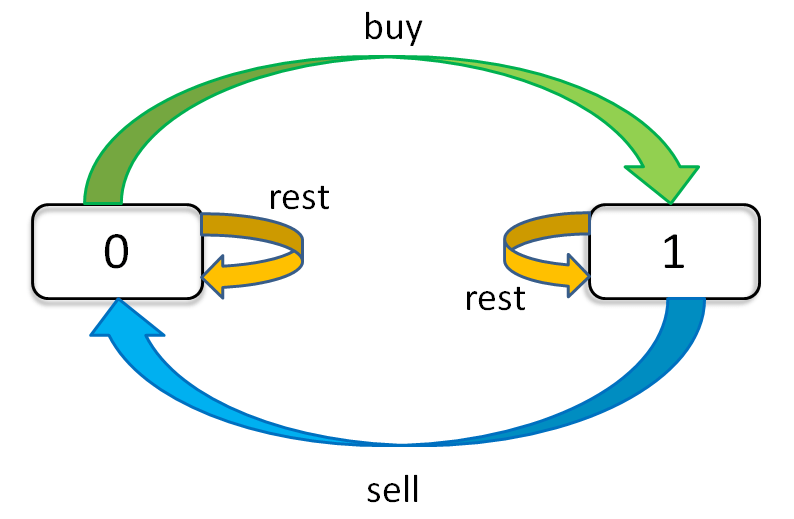
这里有一点需要注意:由于卖出后,需要隔一天才能再次买入。所以,需要保存前一天"为空"状态的值。
参考资料
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
-
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
-
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
Input: [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell] 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
* Runtime: 0 ms, faster than 100.00% of Java online submissions for Best Time to Buy and Sell Stock with Cooldown.
* Memory Usage: 37.9 MB, less than 25.93% of Java online submissions for Best Time to Buy and Sell Stock with Cooldown.
*
* Copy from: https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/solution/yi-ge-fang-fa-tuan-mie-6-dao-gu-piao-wen-ti-by-lab/[一个方法团灭 6 道股票问题 - 最佳买卖股票时机含冷冻期 - 力扣(LeetCode)]
*
* @author D瓜哥 · https://www.diguage.com
* @since 2020-01-28 15:16
*/
public int maxProfit(int[] prices) {
int dp0 = 0;
int dp1 = Integer.MIN_VALUE;
int last = 0;
for (int i = 0; i < prices.length; i++) {
int temp = dp0;
dp0 = Math.max(dp0, dp1 + prices[i]);
dp1 = Math.max(dp1, last - prices[i]); // buy 需要基于前一天基础上。
last = temp;
}
return dp0;
}