友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性:
-
每行的元素从左到右升序排列。
-
每列的元素从上到下升序排列。
示例 1:
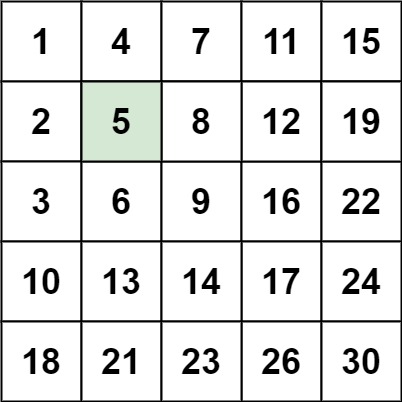
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出:true
示例 2:
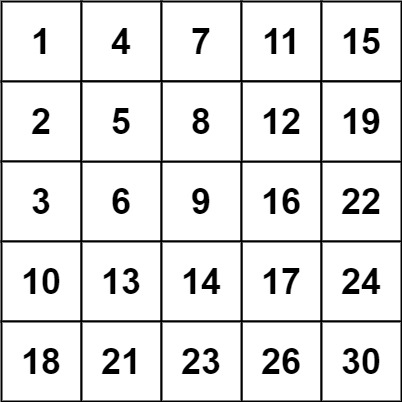
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出:false
提示:
-
m == matrix.length -
n == matrix[i].length -
1 <= n, m <= 300 -
-109 <= matrix[i][j] <= 109 -
每行的所有元素从左到右升序排列
-
每列的所有元素从上到下升序排列
-
-109 <= target <= 109
思路分析
| 不能对整个矩阵进行二分查找!可以对所有行或者列,做二分查找。 |
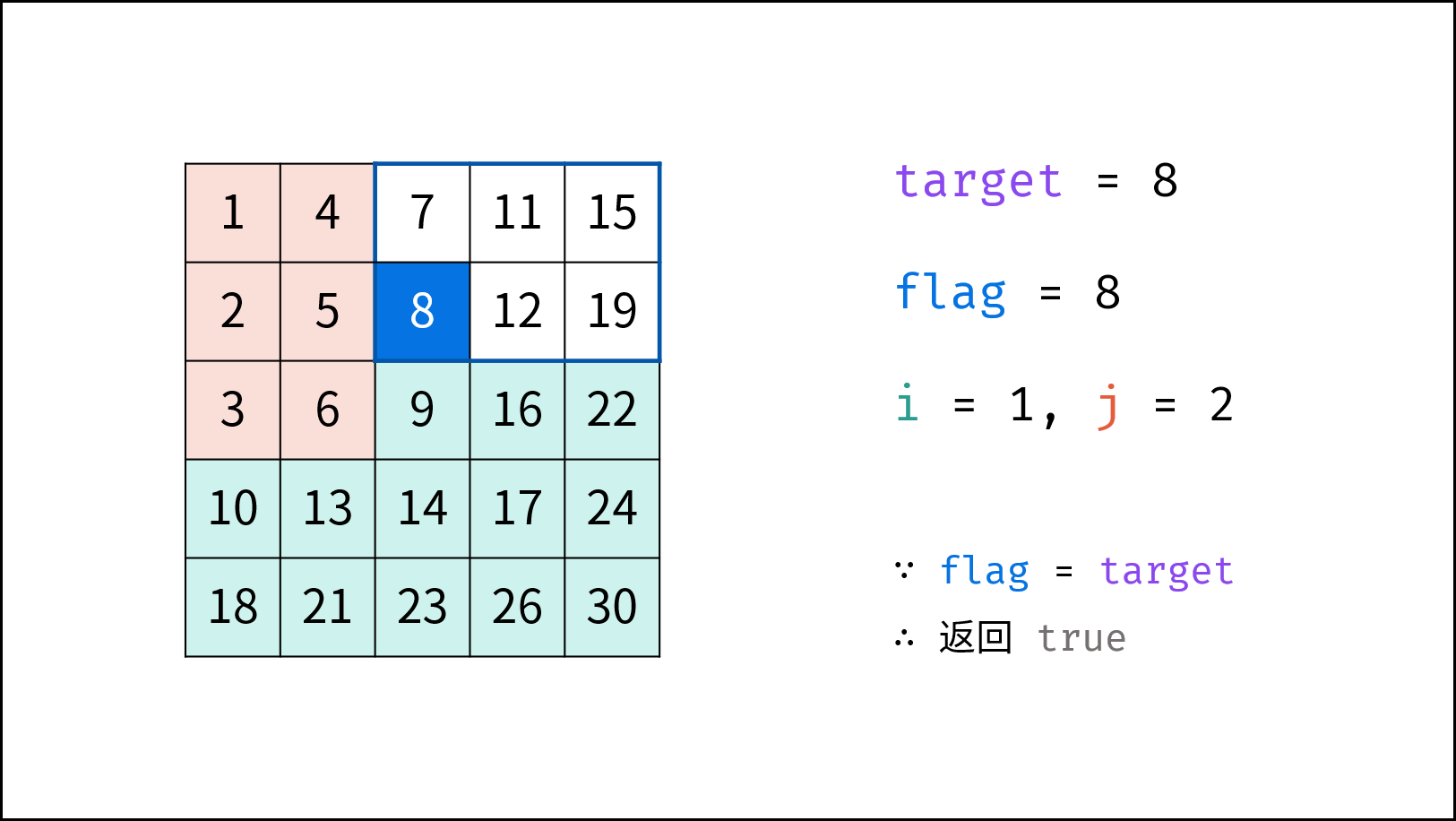
从右上角开始搜索,小于目标值则下移,大于目标值则左移,这个方案真是精妙!
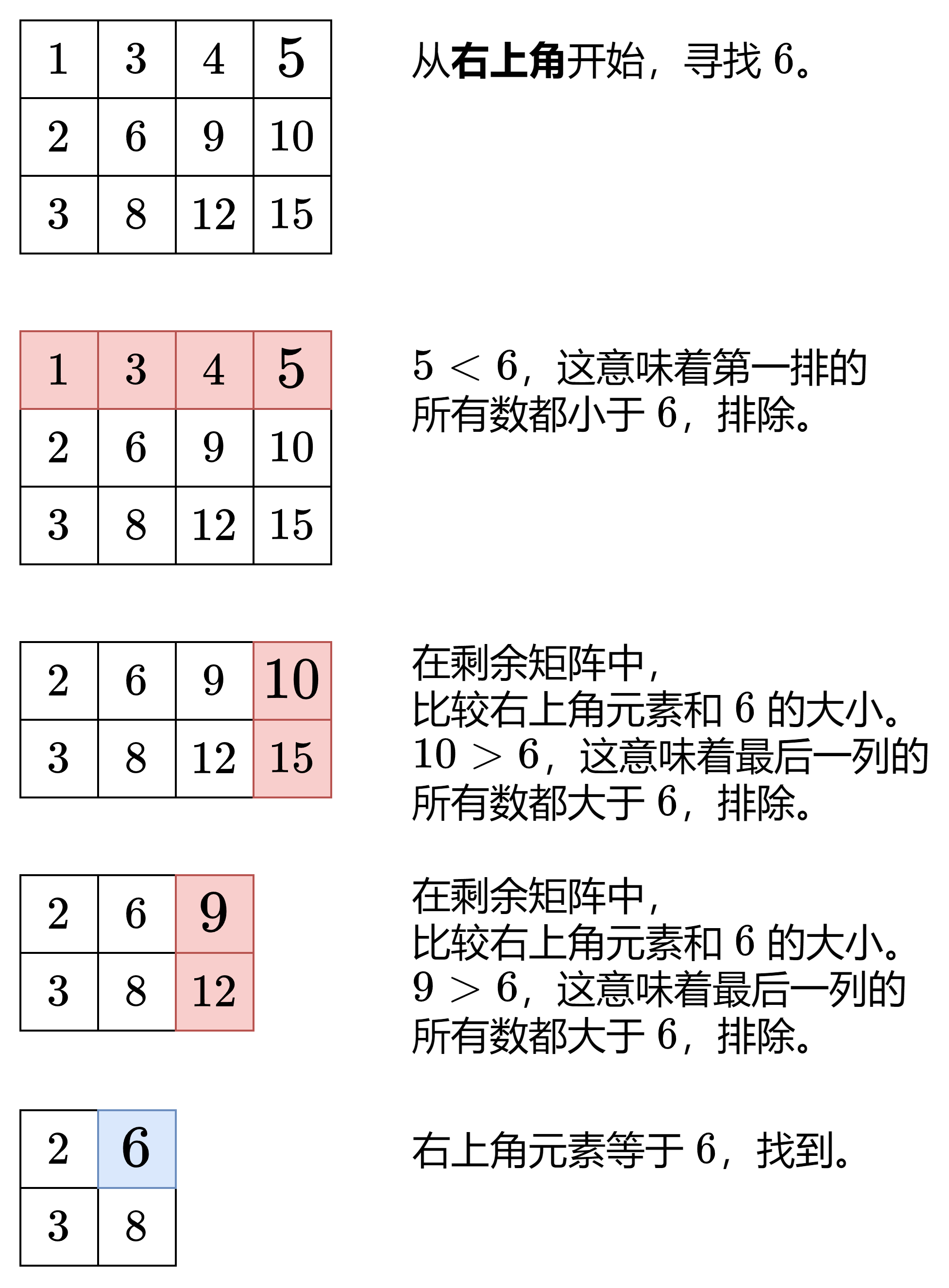
观察矩阵,右上角和左下角的元素有代表性:根据大小,可以删除左边一列(大于等于右上角元素)或上一行(小于等于右上角元素),或者下面一行(大于等于左上角元素)或坐标一列(小于等于左下角元素)。可以根据这个规律,来排查不符合条件的元素。
也可以从左下角开始,小于目标值则右移,大于目标值则上移。
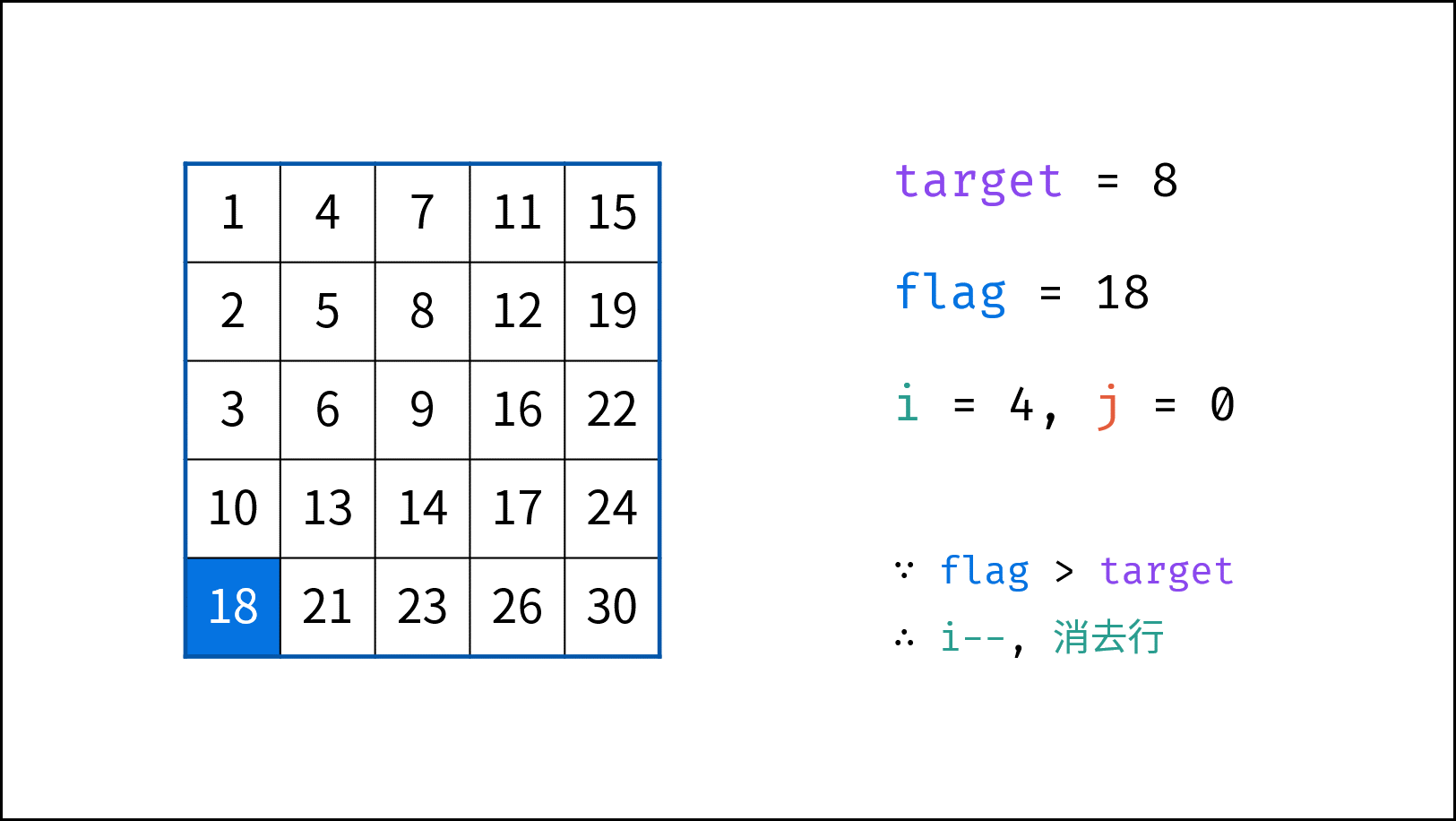
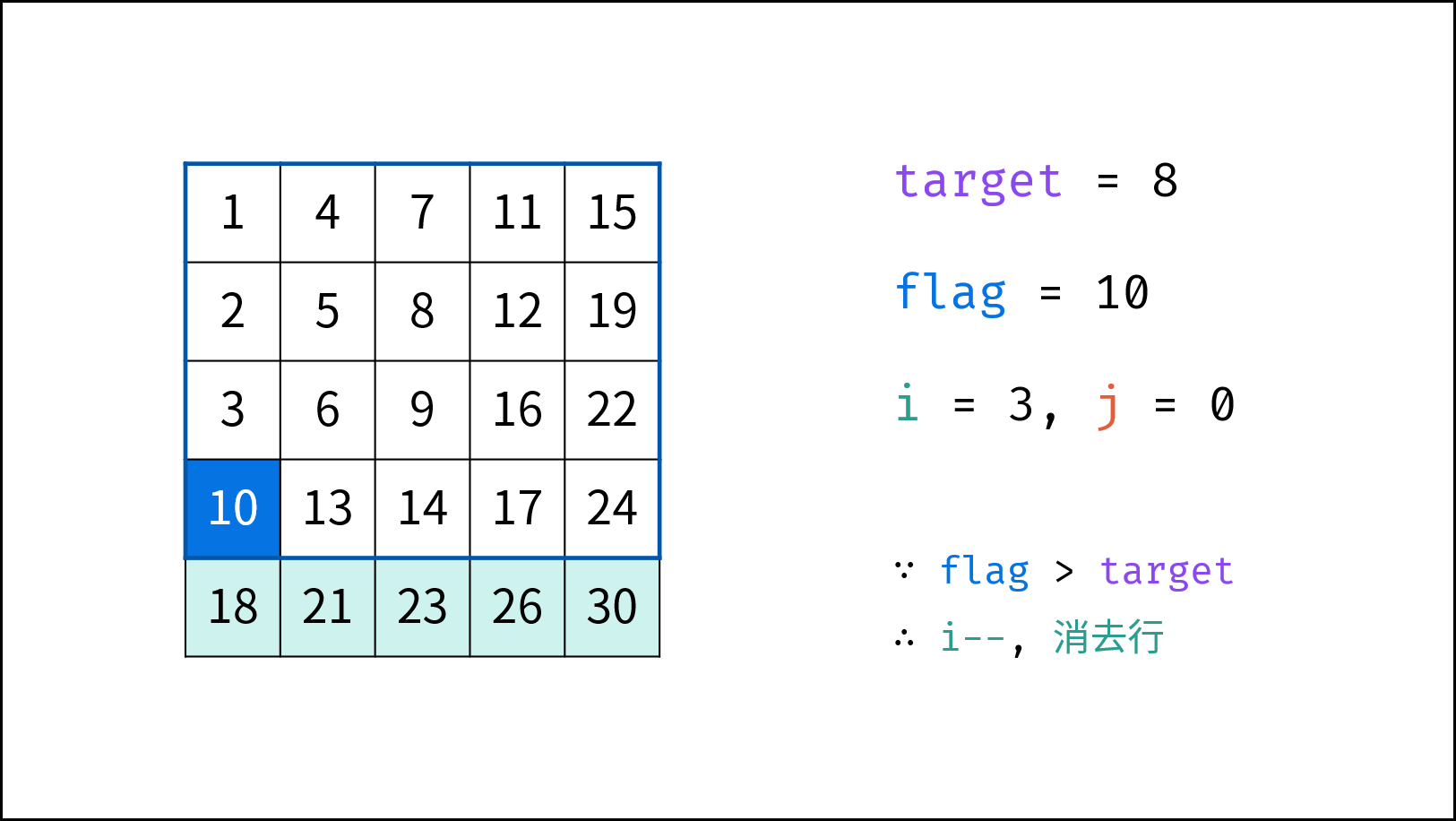
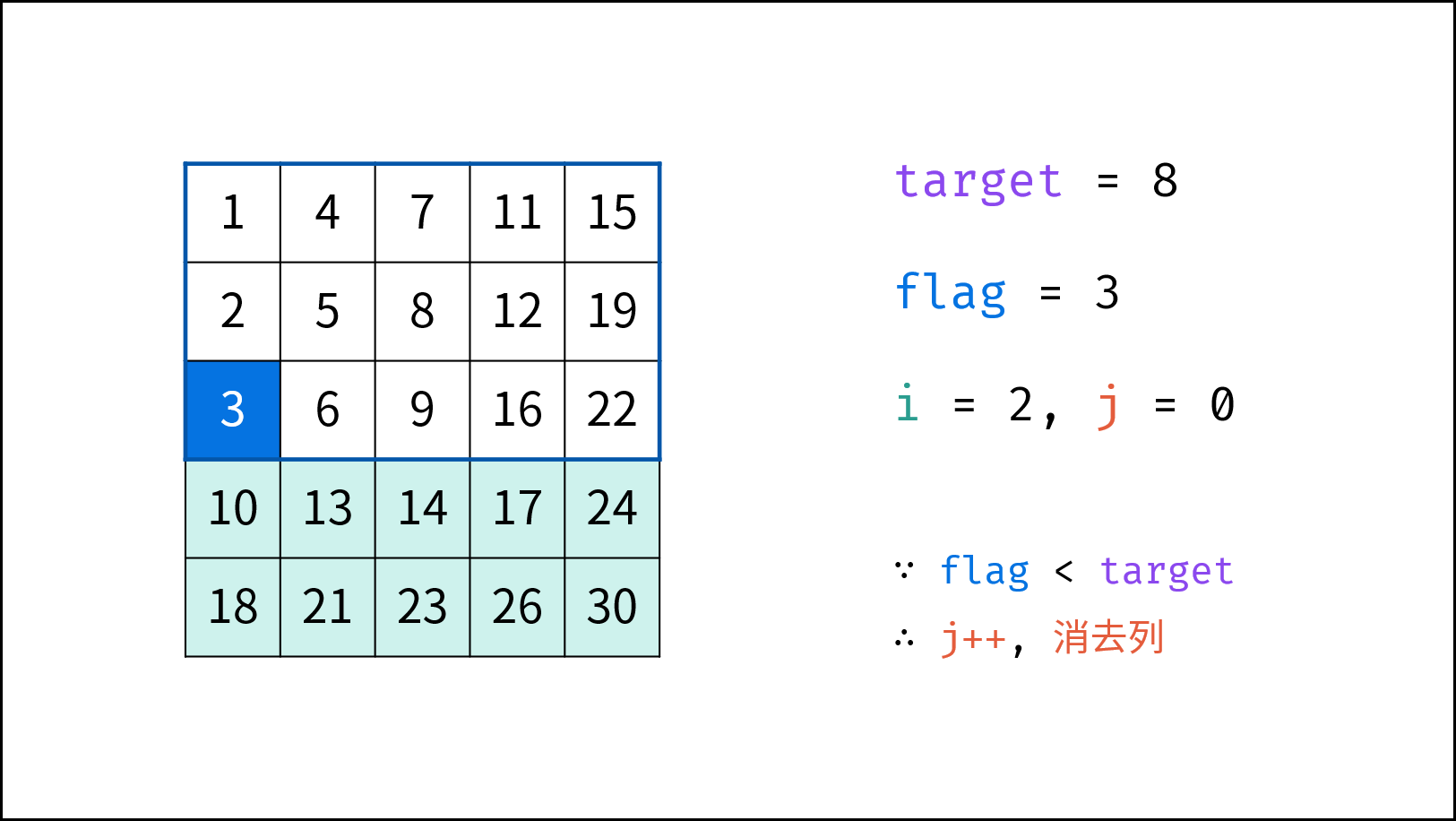
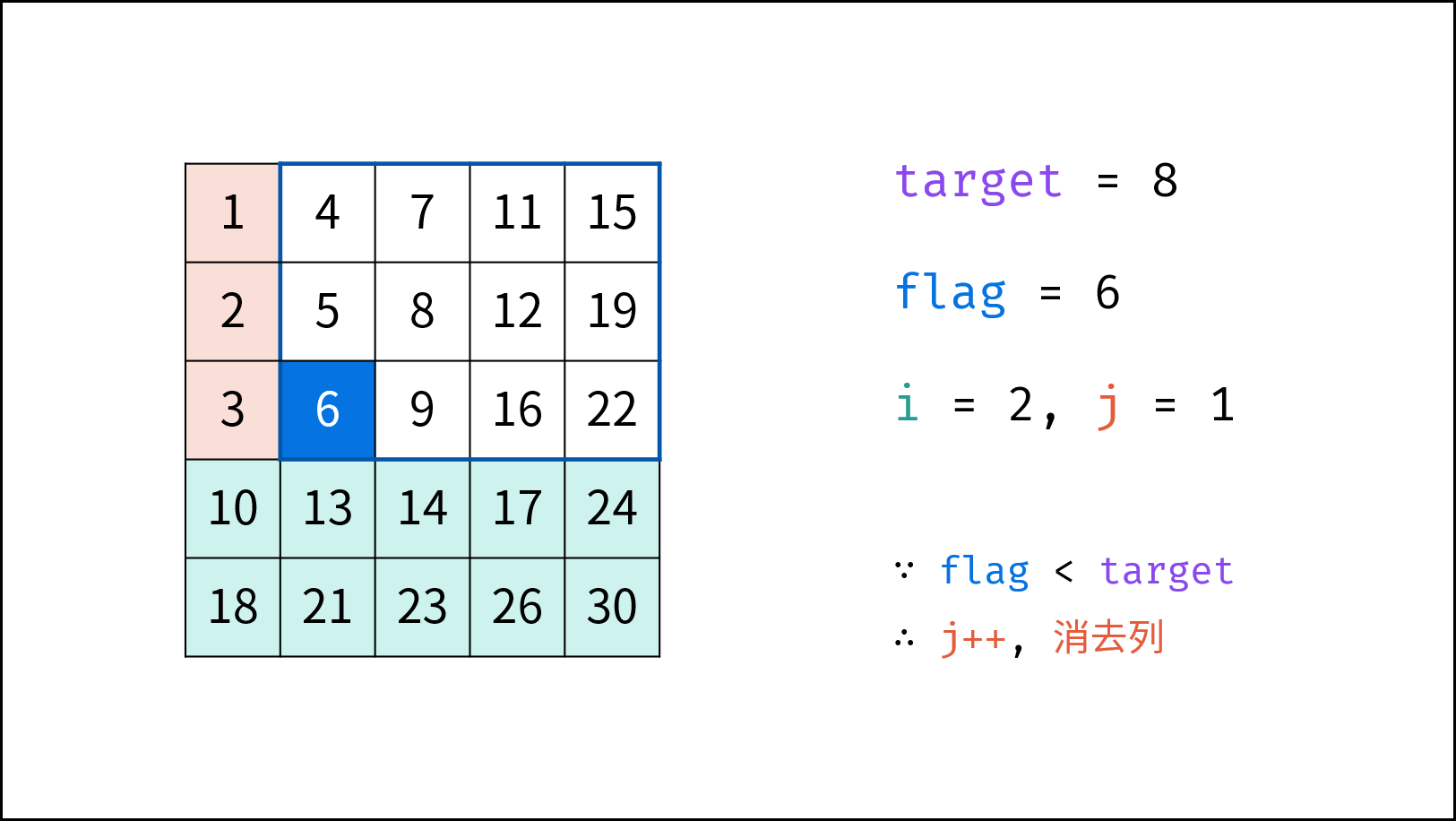
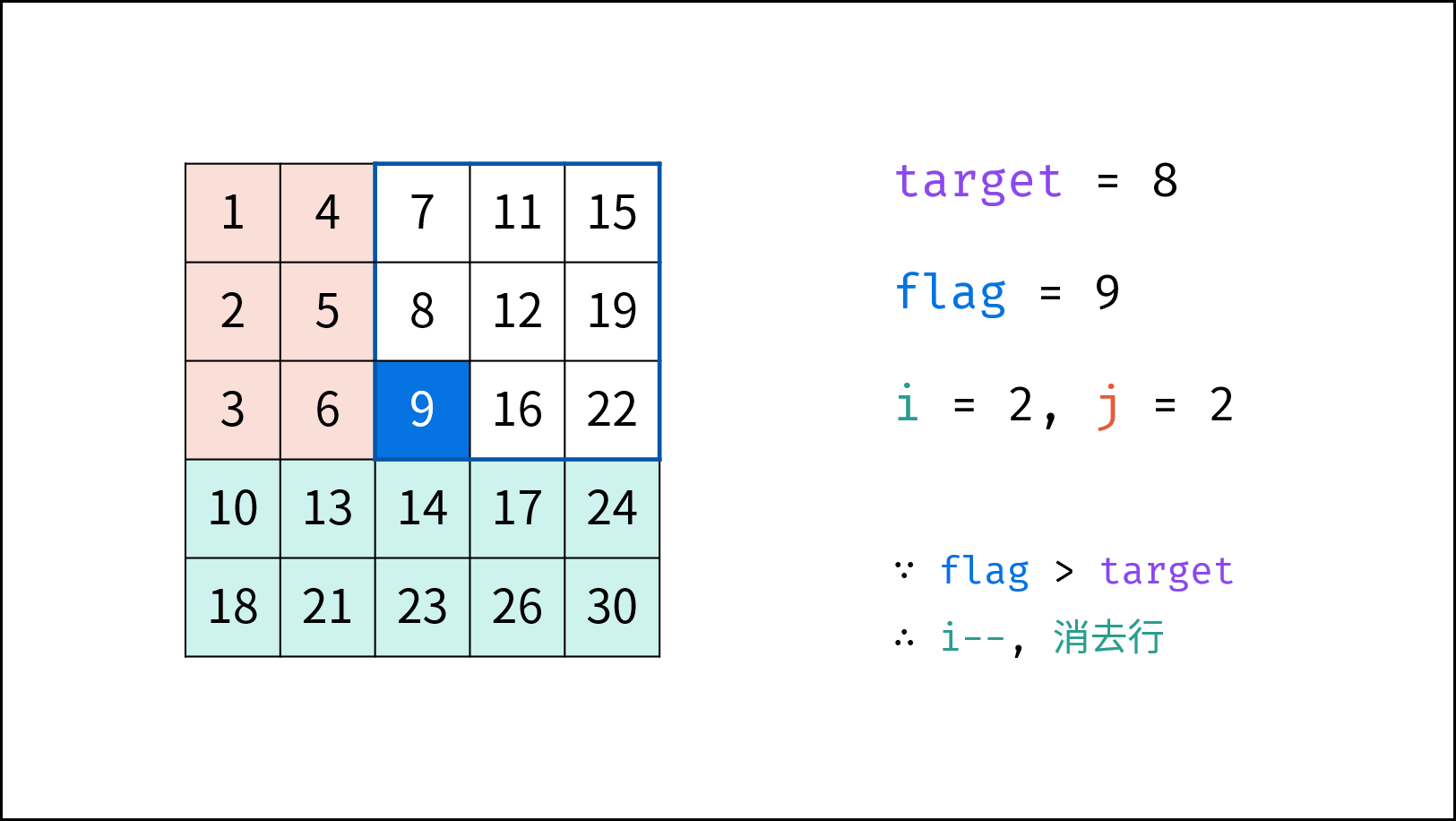
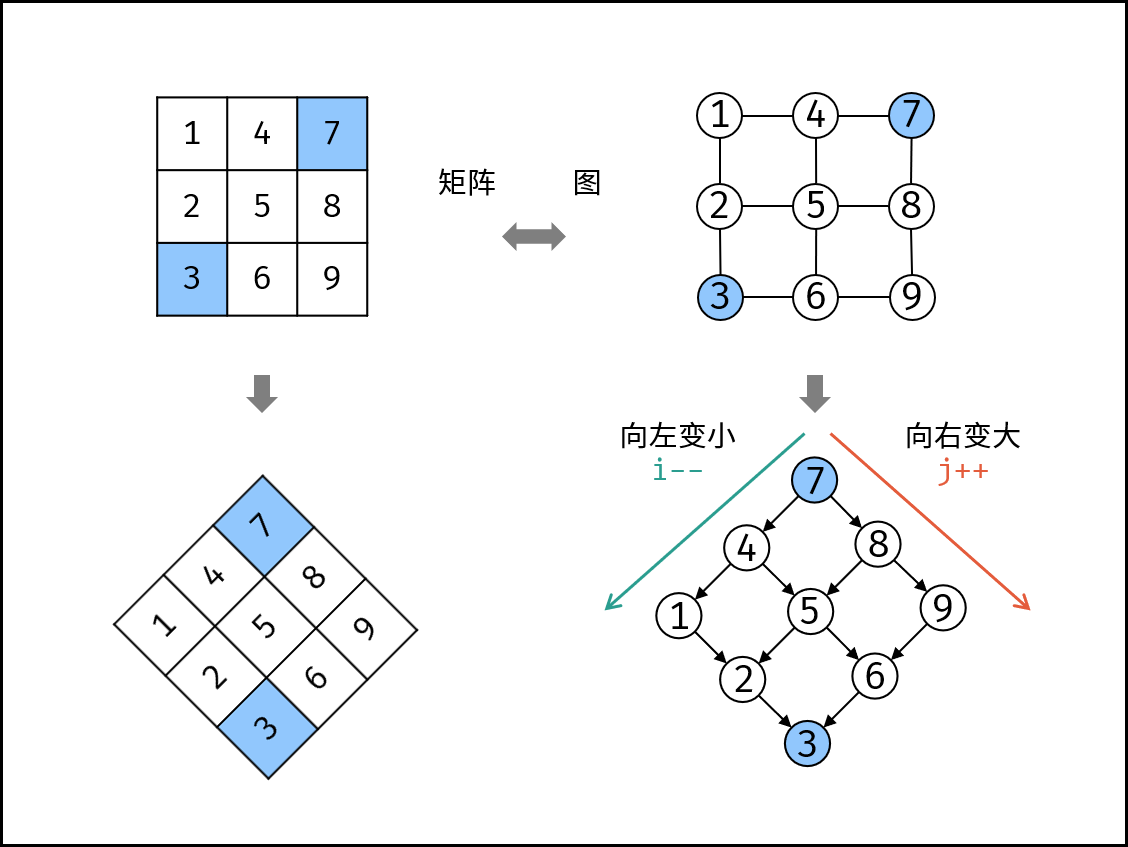
将矩阵旋转一下,会发现上面的解题思路类似于 二叉搜索树,即对于每个元素,其左分支元素更小、右分支元素更大。。因此,通过从 “根节点” 开始搜索,遇到比 target 大的元素就向左,反之向右,即可找到目标值 target。应该更容易理解:
-
一刷
-
二刷
-
三刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
* Runtime: 5 ms, faster than 99.96% of Java online submissions for Search a 2D Matrix II.
*
* Memory Usage: 50.3 MB, less than 5.66% of Java online submissions for Search a 2D Matrix II.
*
* Copy from: https://leetcode.com/problems/search-a-2d-matrix-ii/discuss/66140/My-concise-O(m%2Bn)-Java-solution[(1) My concise O(m+n) Java solution - LeetCode Discuss]
*
* @author D瓜哥 · https://www.diguage.com
* @since 2020-01-23 10:04
*/
public boolean searchMatrix(int[][] matrix, int target) {
if (Objects.isNull(matrix) || matrix.length == 0) {
return false;
}
int column = 0;
int row = matrix[0].length - 1;
while (column < matrix.length && 0 <= row) {
int value = matrix[column][row];
if (value == target) {
return true;
} else if (value < target) {
column++;
} else if (value > target) {
row--;
}
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2024-09-15 18:14:17
*/
public boolean searchMatrix(int[][] matrix, int target) {
int row = 0, column = matrix[0].length - 1;
while (row < matrix.length && 0 <= column) {
int num = matrix[row][column];
if (num == target) {
return true;
} else if (target < num) {
column--;
} else {
row++;
}
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-10-20 20:26:28
*/
public boolean searchMatrix(int[][] matrix, int target) {
int row = 0, column = matrix[row].length - 1;
while (row < matrix.length && column >= 0) {
int num = matrix[row][column];
if (num == target) {
return true;
} else if (target < num) {
column--;
} else {
row++;
}
}
return false;
}

