友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd" 输出:"bb"
提示:
-
1 <= s.length <= 1000 -
s仅由数字和英文字母组成
思路分析
最简单的方式:使用两个指针,把字符串逐个"拆成"子串,然后留下最大子串即可。可惜,这种算法的时间复杂度是 O(n3)。
中心扩散法
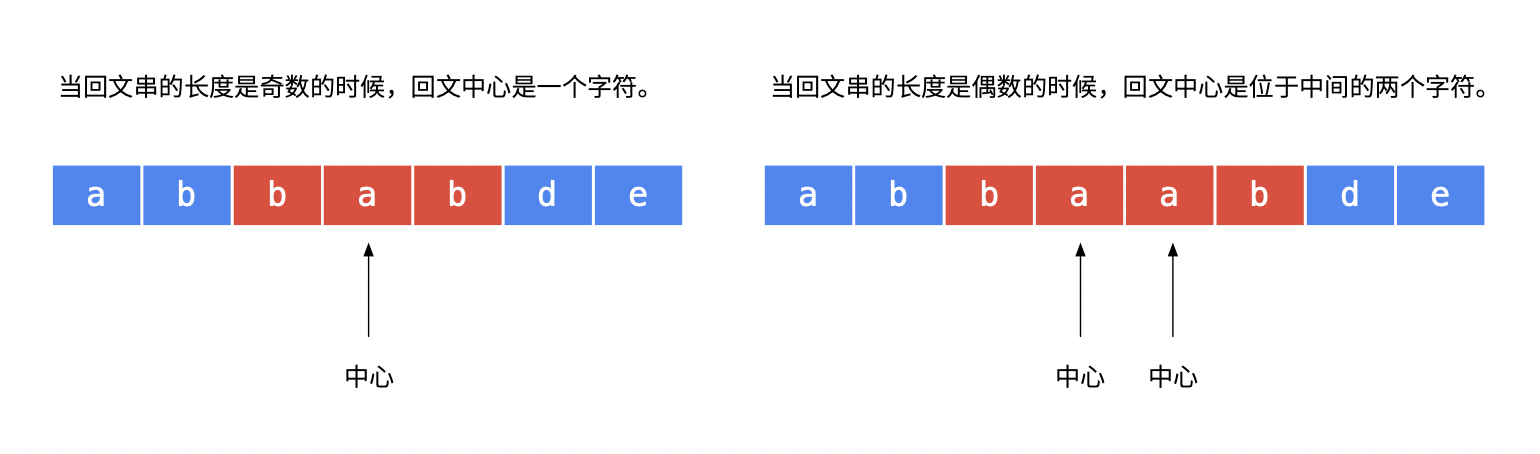
没想到,竟然存在时间复杂度为 O(n) 的算法:Manacher’s Algorithm。在维基百科上有解释: Longest palindromic substring - Wikipedia。回头研究研究再补充!
另外,这道题还可以练手动态规划。
-
一刷
-
二刷
-
三刷
-
四刷
-
五刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/**
* Runtime: 1118 ms, faster than 5.01% of Java online submissions for Longest Palindromic Substring.
*
* Memory Usage: 37.2 MB, less than 94.36% of Java online submissions for Longest Palindromic Substring.
*
* @author D瓜哥 · https://www.diguage.com
* @since 2019-07-13 11:12
*/
public String longestPalindromeBruteForce(String s) {
if (Objects.isNull(s) || s.length() == 1) {
return s;
}
int maxLength = 1;
int begin = 0;
for (int i = 0; i < s.length() - 1; i++) {
for (int j = i + 1; j < s.length(); j++) {
// 这里要注意:先判断长度,然后执行回文判断,相当于做了剪枝操作,效率会提高很多。
if (j - i + 1 > maxLength && isPalindrome(s, i, j)) {
maxLength = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLength);
}
private boolean isPalindrome(String s, int low, int high) {
while (low <= high) {
if (s.charAt(low) != s.charAt(high)) {
return false;
}
low++;
high--;
}
return true;
}
public String longestPalindrome(String s) {
if (Objects.isNull(s) || s.length() <= 1) {
return s;
}
int start = 0;
int end = 0;
for (int i = 0; i < s.length() - 1; i++) {
int len1 = expandAroundCenter(s, i, i);
int len2 = expandAroundCenter(s, i, i + 1);
int len = Math.max(len1, len2);
if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
private int expandAroundCenter(String s, int left, int right) {
while (0 <= left && right < s.length() && s.charAt(left) == s.charAt(right)) {
left--;
right++;
}
return right - left - 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
* 自己实现
*
* @author D瓜哥 · https://www.diguage.com
* @since 2019-07-13 11:12
*/
public String longestPalindrome(String s) {
if (Objects.isNull(s) || s.length() == 1) {
return s;
}
int left = -1, right = -2;
for (int i = 0; i < s.length(); i++) {
boolean p1 = true;
boolean p2 = true;
for (int j = 0; j <= i; j++) {
char c1 = s.charAt(i - j);
// aba 型
if (p1 && i + j < s.length()) {
char c2 = s.charAt(i + j);
if (c1 == c2) {
if ((i + j) - (i - j) > right - left) {
left = i - j;
right = i + j;
}
} else {
p1 = false;
}
}
// aa 型
if (p2 && i + 1 + j < s.length()) {
char c2 = s.charAt(i + 1 + j);
if (c2 == c1) {
if ((i + 1 + j) - (i - j) > right - left) {
left = i - j;
right = i + 1 + j;
}
} else {
p2 = false;
}
}
if (!p1 && !p2) {
break;
}
}
}
return left >= 0 ? s.substring(left, right + 1) : null;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/**
* 相仿 718 题的思路。
*
* TODO 解法还有少许缺陷:142个用例,通过了140个。
* abcdbbfcba 找不到合适的回文字符串。
*
* @author D瓜哥 · https://www.diguage.com
* @since 2024-10-08 14:22:42
*/
public String longestPalindrome(String s) {
if (Objects.isNull(s) || s.length() == 1) {
return s;
}
return findMax(s, new StringBuilder(s).reverse().toString());
}
private String findMax(String a, String b) {
int length = b.length();
String result = "";
// 处理 a 的头部 与 b 的尾部 的字符串
for (int len = 1; len <= length; len++) {
String temp = maxLength(a, 0, b, length - len, len);
if (temp.length() > result.length() && isPalindromic(temp)) {
result = temp;
}
}
// 由于两个字符串长度相同,则不需要处理中间对其部分的处理
// 这里的代码假设,a 短 b 长
// for (int i = b.length() - a.length(); i >= 0; i--) {
// String temp = maxLength(a, 0, b, i, a.length());
// }
// 处理 a 的尾部 与 b 的头部
for (int i = 1; i < length; i++) {
String temp = maxLength(a, i, b, 0, length - i);
if (temp.length() > result.length() && isPalindromic(temp)) {
result = temp;
}
}
return result.isEmpty() ? null : result;
}
private String maxLength(String a, int as, String b, int bs, int len) {
int count = 0;
StringBuilder temp = new StringBuilder();
String result = "";
for (int i = 0; i < len; i++) {
if (a.charAt(as + i) == b.charAt(bs + i)) {
count++;
temp.append(a.charAt(as + i));
if (temp.length() > result.length()) {
result = temp.toString();
}
} else if (count > 0) {
count = 0;
temp = new StringBuilder();
}
}
int sn = a.length();
System.out.println(String.format("%3d %3d %3d %" + (as + len != a.length() ? "-" : "")
+ sn + "s %" + (as + len == a.length() ? "-" : "") + sn + "s" + " %" + sn + "s",
as, bs, len, a.substring(as, as + len), b.substring(bs, bs + len), result));
return result;
}
private boolean isPalindromic(String s) {
int l = 0, r = s.length() - 1;
while (l < r) {
if (s.charAt(l) != s.charAt(r)) {
return false;
}
l++;
r--;
}
return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-05 23:47:51
*/
public String longestPalindrome(String s) {
String result = "";
for (int i = 0; i < s.length(); i++) {
String p = getPalindrome(s, i);
if (result.length() < p.length()) {
result = p;
}
}
return result;
}
private String getPalindrome(String s, int idx) {
String result = "";
int l = idx, r = idx;
while (0 <= l && r < s.length() && s.charAt(l) == s.charAt(r)) {
if (result.length() < r - l + 1) {
result = s.substring(l, r + 1);
}
l--;
r++;
}
l = idx;
r = idx + 1;
while (0 <= l && r < s.length() && s.charAt(l) == s.charAt(r)) {
if (result.length() < r - l + 1) {
result = s.substring(l, r + 1);
}
l--;
r++;
}
return result;
}
// /**
// * 可以从两头判断:如果两头相等,则判断是否为回文,如果是中止循环。
// *
// * 可惜效率并不高。
// */
// private String getPalindrome(String s, int idx) {
// String result = "";
// int len = Math.min(idx - 0, s.length() - idx - 1);
// int l = idx - len, r = idx + len;
// while (l <= r) {
// if (s.charAt(l) == s.charAt(r) && isPalindrome(s, l, r)) {
// break;
// }
// l++;
// r--;
// }
// result = s.substring(l, r + 1);
// len = Math.min(idx - 0, (s.length() - 1) - (idx + 1));
// l = idx - len;
// r = idx + 1 + len;
// while (l < r) {
// if (s.charAt(l) == s.charAt(r) && isPalindrome(s, l, r)) {
// break;
// }
// l++;
// r--;
// }
// if (result.length() < r - l + 1) {
// result = s.substring(l, r + 1);
// }
// return result;
// }
//
// private boolean isPalindrome(String s, int left, int ritht) {
// while (left < ritht) {
// if (s.charAt(left++) != s.charAt(ritht--)) {
// return false;
// }
// }
// return true;
// }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-12-05 21:52:24
*/
public String longestPalindrome(String s) {
String result = "";
for (int i = 0; i < s.length(); i++) {
String palindrome = longestPalindrome(s, i);
if (palindrome.length() > result.length()) {
result = palindrome;
}
}
return result;
}
private String longestPalindrome(String s, int mid) {
String result = "";
for (int i = 0; i <= mid && mid + i < s.length(); i++) {
int left = mid - i;
int right = mid + i;
if (s.charAt(left) != s.charAt(right)) {
break;
}
if (result.length() < (right - left + 1)) {
result = s.substring(left, right + 1);
}
}
for (int i = 0; i <= mid && mid + 1 + i < s.length(); i++) {
int left = mid - i;
int right = mid + 1 + i;
if (s.charAt(left) != s.charAt(right)) {
break;
}
if (result.length() < (right - left + 1)) {
result = s.substring(left, right + 1);
}
}
return result;
}
参考资料
-
Manacher’s Algorithm - Linear Time Longest Palindromic Substring - Part 1
-
Manacher’s Algorithm - Linear Time Longest Palindromic Substring - Part 2
-
Manacher’s Algorithm - Linear Time Longest Palindromic Substring - Part 3
-
Manacher’s Algorithm - Linear Time Longest Palindromic Substring - Part 4
-
Manacher’s Algorithm Explained— Longest Palindromic Substring

