友情支持
如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜
|
|
有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。
公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
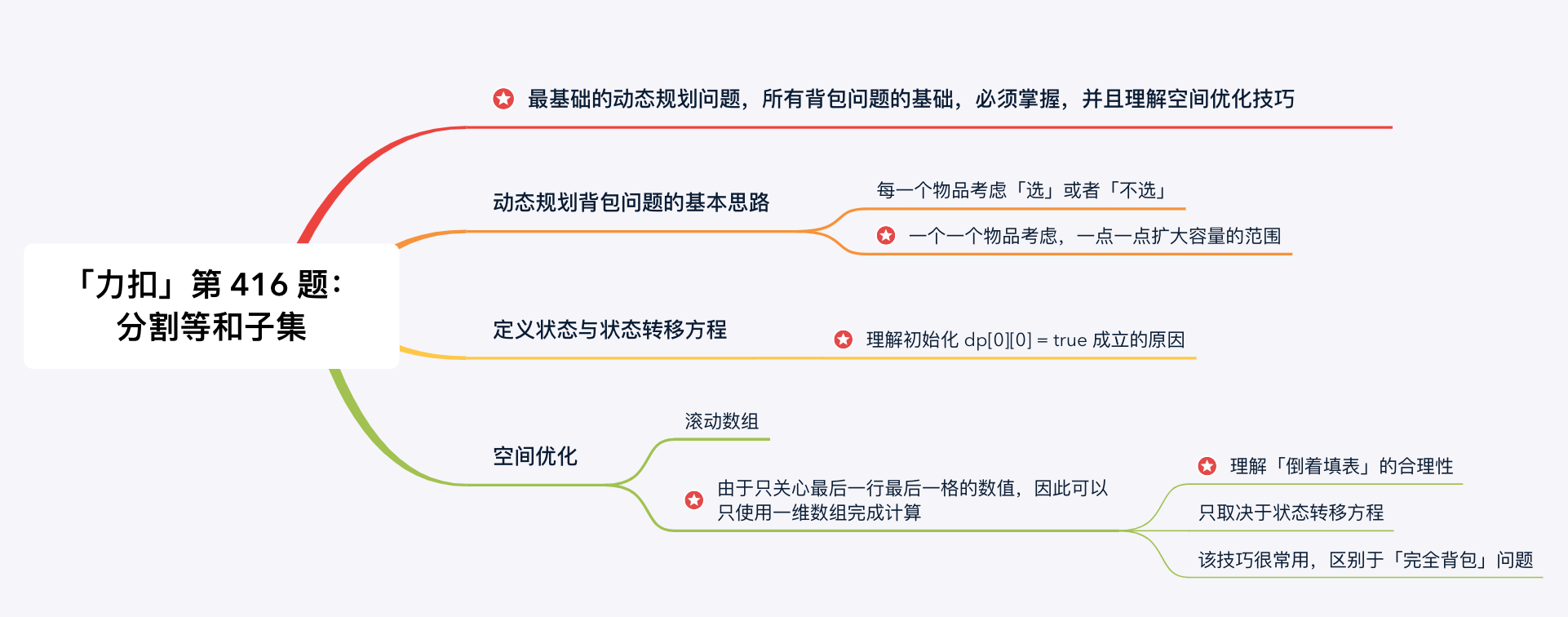
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
示例 1：
输入：nums = [1,5,11,5] 输出：true 解释：数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2：
输入：nums = [1,2,3,5] 输出：false 解释：数组不能分割成两个元素和相等的子集。
提示：
-
1 <= nums.length <= 200 -
1 <= nums[i] <= 100
思路分析
这道题使用回溯法更容易理解，也更高效。
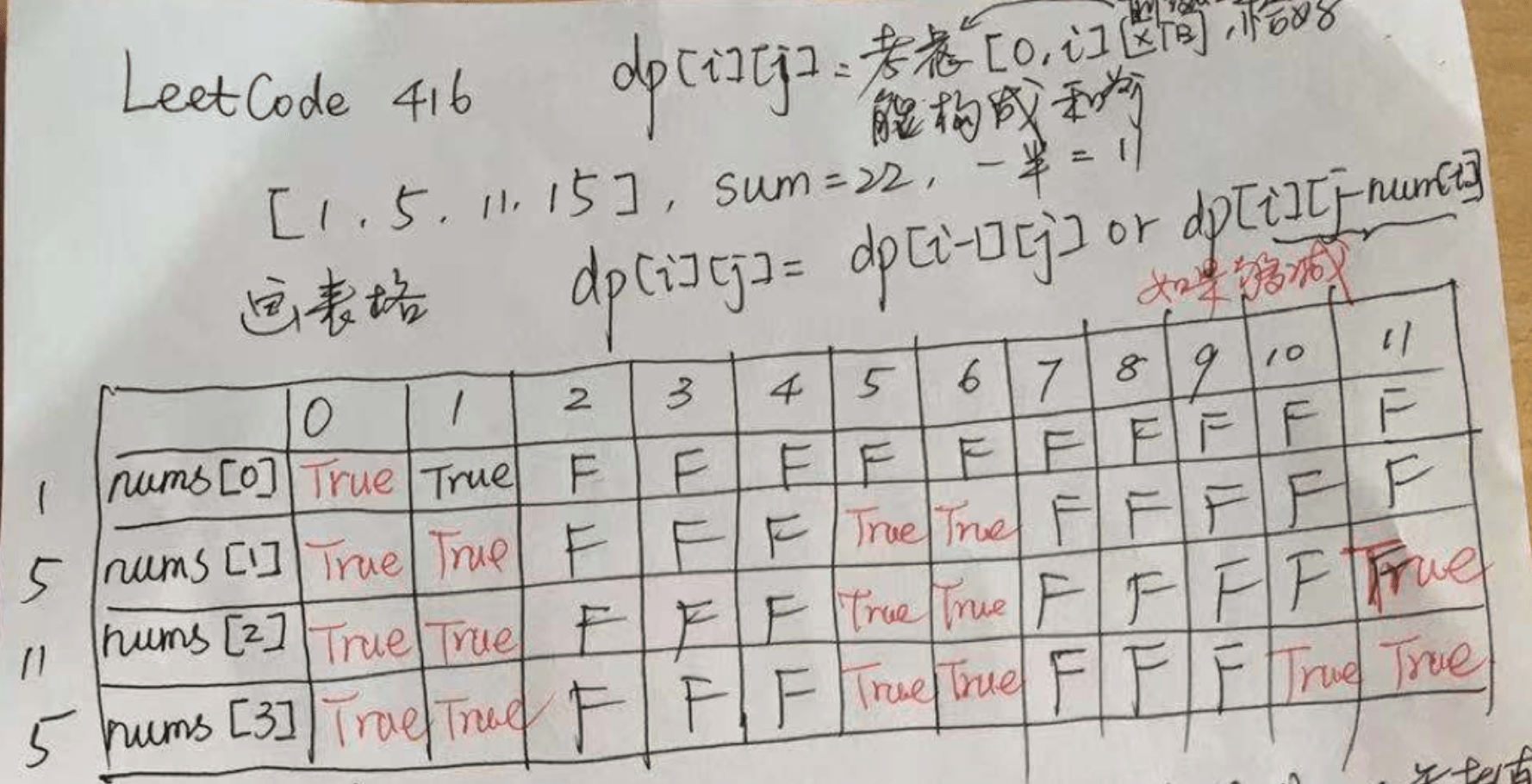
建议动笔计算，手动模拟填表的过程，其实就是画表格。这个过程非常重要，自己动手填过表，更能加深体会程序是如何执行的，也能更好地理解「空间优化」技巧的思路和好处。
-
一刷
-
二刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/**
* Runtime: 10 ms, faster than 72.90% of Java online submissions for Partition Equal Subset Sum.
* Memory Usage: 37.8 MB, less than 50.79% of Java online submissions for Partition Equal Subset Sum.
*
* https://leetcode-cn.com/problems/partition-equal-subset-sum/solution/0-1-bei-bao-wen-ti-xiang-jie-zhen-dui-ben-ti-de-yo/[动态规划（0-1 背包问题） - 分割等和子集 - 力扣（LeetCode）]
*
* @author D瓜哥 · https://www.diguage.com
* @since 2020-01-29 19:30
*/
public boolean canPartitionDp(int[] nums) {
if (Objects.isNull(nums) || nums.length == 0) {
return false;
}
int sum = 0;
for (int num : nums) {
sum += num;
}
if ((sum & 1) == 1) {
return false;
}
int target = sum / 2;
boolean[] dp = new boolean[target + 1];
dp[0] = true;
if (nums[0] <= target) {
dp[nums[0]] = true;
}
for (int i = 1; i < nums.length; i++) {
for (int j = target; nums[i] <= j; j--) {
if (dp[target]) {
return true;
}
dp[j] = dp[j] || dp[j - nums[i]];
}
}
return dp[target];
}
/**
* Runtime: 2 ms, faster than 91.78% of Java online submissions for Partition Equal Subset Sum.
* Memory Usage: 39.6 MB, less than 6.35% of Java online submissions for Partition Equal Subset Sum.
*
* Copy from: https://leetcode-cn.com/problems/partition-equal-subset-sum/solution/java-hui-su-fa-jie-fa-2ms-by-wang_dong/[java 回溯法解法 2ms - 分割等和子集 - 力扣（LeetCode）]
*/
public boolean canPartition(int[] nums) {
if (Objects.isNull(nums) || nums.length == 0) {
return true;
}
int sum = 0;
for (int num : nums) {
sum += num;
}
if ((sum & 1) == 1) {
return false;
}
Arrays.sort(nums);
reverse(nums);
return canPartition(nums, sum / 2, 0);
}
private boolean canPartition(int[] nums, int target, int index) {
if (index >= nums.length || nums[index] > target) {
return false;
}
if (nums[index] == target) {
return true;
}
return canPartition(nums, target - nums[index], index + 1)
|| canPartition(nums, target, index + 1);
}
private void reverse(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
left++;
right--;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
* 动态规划，没有优化空间
*
* @author D瓜哥 · https://www.diguage.com
* @since 2024-09-03 19:13:39
*/
public boolean canPartition(int[] nums) {
int sum = Arrays.stream(nums).sum();
// 特判：如果是奇数，就不符合要求
if (sum % 2 != 0) {
return false;
}
int length = nums.length;
int target = sum / 2;
// 创建二维状态数组，行：物品索引，列：容量（包括 0）
// dp[i][j] 表示从数组的 [0, i] 这个子区间内挑选一些正整数，
// 每个数只能用一次，使得这些数的和恰好等于 j。
boolean[][] dp = new boolean[length][target + 1];
// 先填表格第 0 行，第 1 个数只能让容积为它自己的背包恰好装满
if (nums[0] < target) {
dp[0][nums[0]] = true;
}
for (int i = 1; i < length; i++) {
for (int j = 0; j <= target; j++) {
// 注：这里的 j 就相当于背包的容量
// 直接从上一行先把结果抄下来，然后再修正
dp[i][j] = dp[i - 1][j];
if (nums[i] == j) {
dp[i][j] = true;
} else if (nums[i] < j) {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
}
}
}
return dp[length - 1][target];
}