友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
1644. Lowest Common Ancestor of a Binary Tree II
Given the root of a binary tree, return the lowest common ancestor (LCA) of two given nodes, p and q. If either node p or q does not exist in the tree, return null. All values of the nodes in the tree are unique.
According to the definition of LCA on Wikipedia: "The lowest common ancestor of two nodes p and q in a binary tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself)". A descendant of a node x is a node y that is on the path from node x to some leaf node.
Example 1:
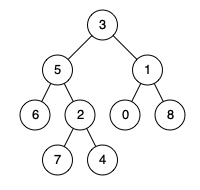
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.Example 2:
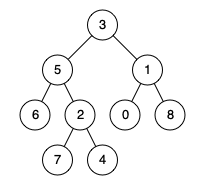
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5. A node can be a descendant of itself according to the definition of LCA.Example 3:
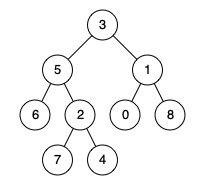
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 10
Output: null
Explanation: Node 10 does not exist in the tree, so return null.Constraints:
The number of nodes in the tree is in the range [1, 104]. -109 ⇐ Node.val ⇐ 109 All Node.val are unique. p != q
思路分析
-
一刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2024-07-26 20:00:58
*
* TODO 没有验证!
*/
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Result result = dfs(root, p, q);
return result.findP && result.findQ ? result.node : null;
}
private Result dfs(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) {
return new Result(null, false, false);
}
Result left = dfs(root.left, p, q);
Result right = dfs(root.right, p, q);
if (left.node != null && right.node != null) {
return new Result(root, true, true);
}
if (root.val == p.val || root.val == q.val) {
boolean findP = false;
if (root.val == p.val) {
findP = true;
}
boolean findQ = false;
if (root.val == q.val) {
findQ = true;
}
return new Result(root,
findP || left.findP || right.findP,
findQ || left.findQ || right.findQ);
}
return left.node != null ? left : right;
}
public static class Result {
TreeNode node;
boolean findP;
boolean findQ;
public Result() {
}
public Result(TreeNode node, boolean findP, boolean findQ) {
this.node = node;
this.findP = findP;
this.findQ = findQ;
}
}

