友情支持

如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜

支付宝

微信

有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。

wx jikerizhi

公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。

117. 填充每个节点的下一个右侧节点指针 II

LeetCode - 117. 填充每个节点的下一个右侧节点指针 II

给定一个二叉树：

struct Node {
  int val;
  Node left;
  Node right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

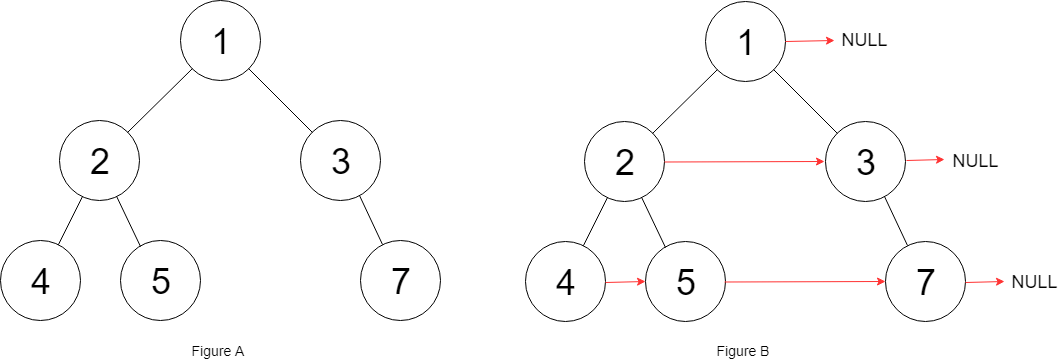
0117 1 
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

示例 2：

输入：root = []
输出：[]

提示：

  • 树中的节点数在范围 [0, 6000] 内

  • -100 <= Node.val <= 100

进阶：

  • 你只能使用常量级额外空间。

  • 使用递归解题也符合要求，本题中递归程序的隐式栈空间不计入额外空间复杂度。

思路分析

这道题和 116. Populating Next Right Pointers in Each Node 算是姊妹题。

最简单的方式，使用 Deque 来保存每一层节点，然后建立起来"连接"。但是，很明显，这种方案不符合空间复杂度要求。

基于上面这种解法，再深入思考一步，上面使用 Deque 就是想要保存接下来需要访问的元素，并且保存访问的前后顺序。现在 Node 上有 next 字段，可以利用这个字段，打通这条链表，遍历上一层时，打通下一次的链接结构。这里需要保存的就有两点：

  1. 这条链表的头结点，用于下一层的遍历；

  2. 这条链表的尾节点，用于添加下一个节点。

这道题的思路和 116. Populating Next Right Pointers in Each Node 思路几乎是一样的：在上层遍历中，建立下一层的链接。

但这道题和 116. Populating Next Right Pointers in Each Node 在于：116 是完全二叉树，那么可以直接使用 next 节点的 left 子节点。这道题不是一个完全二叉树，所以，就需要在运动中寻找不为空的节点。另外，最左节点的选择，也不能直接使用 mostLeft.left，也是需要在运动中去寻找下一层第一个不为空的节点。两道题区别不大只是需要多注意细节。

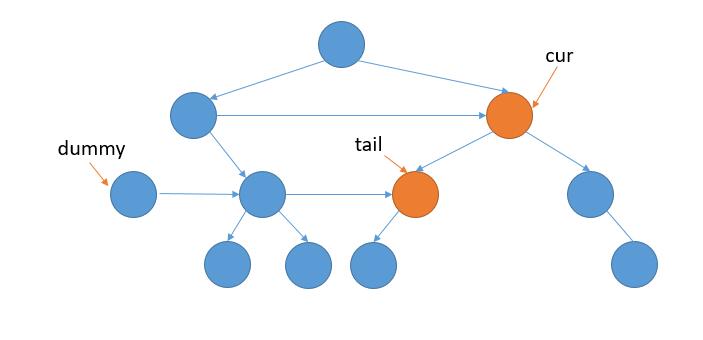
0117 2

这样，把第一种解法的代码稍作修改就可以了。

看题解，别人大部分是用了两层循环，外层是负责向下推进，内层负责同层向右。D瓜哥用了一层循环来遍历每个节点。

  • 一刷

  • 二刷

  • 二刷（优化）

  • 三刷

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2020-02-09 23:17
 */
static class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node(int x) {
        this.val = x;
    }

    @Override
    public String toString() {
        return "Node{" +
                "val=" + val +
                ", left=" + left +
                ", right=" + right +
                '}';
    }
}


/**
 * Runtime: 1 ms, faster than 49.14% of Java online submissions for Populating Next Right Pointers in Each Node II.
 * Memory Usage: 41.4 MB, less than 100.00% of Java online submissions for Populating Next Right Pointers in Each Node II.
 *
 * Copy from: https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-28/[详细通俗的思路分析，多解法 - 填充每个节点的下一个右侧节点指针 II - 力扣（LeetCode）]
 */
public Node connect(Node root) {
    Node curr = root;
    while (Objects.nonNull(curr)) {
        Node dummy = new Node(0);
        Node tail = dummy;
        while (Objects.nonNull(curr)) {
            if (Objects.nonNull(curr.left)) {
                tail.next = curr.left;
                tail = tail.next;
            }
            if (Objects.nonNull(curr.right)) {
                tail.next = curr.right;
                tail = tail.next;
            }
            curr = curr.next;
        }
        curr = dummy.next;
    }
    return root;
}

/**
 * Runtime: 1 ms, faster than 49.14% of Java online submissions for Populating Next Right Pointers in Each Node II.
 * Memory Usage: 40.8 MB, less than 100.00% of Java online submissions for Populating Next Right Pointers in Each Node II.
 */
public Node connectDeque(Node root) {
    if (Objects.isNull(root)) {
        return null;
    }
    Deque<Node> deque = new LinkedList<>();
    deque.addLast(root);
    Node prev = null;
    while (!deque.isEmpty()) {
        int size = deque.size();
        for (int i = 0; i < size; i++) {
            Node curr = deque.removeFirst();
            if (Objects.nonNull(curr.left)) {
                deque.addLast(curr.left);
            }
            if (Objects.nonNull(curr.right)) {
                deque.addLast(curr.right);
            }
            if (i > 0) {
                prev.next = curr;
            }
            prev = curr;
        }
    }
    return root;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2024-06-25 17:26:18
 */
public Node connect(Node root) {
  if (root == null) {
    return null;
  }
  Queue<Node> queue = new LinkedList<>();
  queue.offer(root);
  while (!queue.isEmpty()) {
    int size = queue.size();
    Node pre = null;
    for (int i = 0; i < size; i++) {
      Node cur = queue.poll();
      if (pre != null) {
        pre.next = cur;
      }
      if (cur.left != null) {
        queue.offer(cur.left);
      }
      if (cur.right != null) {
        queue.offer(cur.right);
      }
      pre = cur;
    }
  }
  return root;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2024-06-25 17:26:18
 */
public Node connect(Node root) {
  if (root == null) {
    return null;
  }
  Node mostLeft = root;
  while (mostLeft != null) {
    Node cur = mostLeft;
    mostLeft = null;
    Node prev = null;
    while (cur != null) {
      if (cur.left != null) {
        // 不能保证左子树的最节点就一定有值
        // 所以，在运动中，寻找最左节点
        if (mostLeft == null) {
          mostLeft = cur.left;
        }
        // 由于不是完全二叉树，
        // 所以需要在运动中寻找不为空的节点
        if (prev != null) {
          prev.next = cur.left;
          prev = prev.next;
        } else {
          prev = cur.left;
        }
      }
      if (cur.right != null) {
        // 不能保证左子树的最节点就一定有值
        // 所以，在运动中，寻找最左节点
        if (mostLeft == null) {
          mostLeft = cur.right;
        }
        // 由于不是完全二叉树，
        // 所以需要在运动中寻找不为空的节点
        if (prev != null) {
          prev.next = cur.right;
          prev = prev.next;
        } else {
          prev = cur.right;
        }
      }
      cur = cur.next;
    }
  }
  return root;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

/**
 * @author D瓜哥 · https://www.diguage.com
 * @since 2025-06-04 21:38:37
 */
public Node connect(Node root) {
  if (root == null) {
    return root;
  }
  Node cur = root;
  Node mostLeft = root;
  Node prev = null;
  while (cur != null) {
    // 寻找下一层最左节点
    if (cur == mostLeft || mostLeft == null) {
      mostLeft = cur.left;
      if (mostLeft == null) {
        mostLeft = cur.right;
      }
    }
    if (prev != null) {
      if (cur.left != null) {
        prev.next = cur.left;
        prev = prev.next;
      }
      if (cur.right != null) {
        prev.next = cur.right;
        prev = prev.next;
      }
    } else {
      if (cur.left != null) {
        prev = cur.left;
      }
      if (cur.right != null) {
        if (prev != null) {
          prev.next = cur.right;
          prev = prev.next;
        } else {
          prev = cur.right;
        }
      }
    }
    if (cur.next != null) {
      cur = cur.next;
    } else {
      cur = mostLeft;
      prev = null;
    }
  }
  return root;
}

参考资料

  1. 详细通俗的思路分析，多解法 - 填充每个节点的下一个右侧节点指针 II

  2. 117. 填充每个节点的下一个右侧节点指针 II

  3. 117. 填充每个节点的下一个右侧节点指针 II - 三种方法：DFS/BFS/BFS+链表（附题单）

← Previous: 116. Populating Next Right Pointers in Each Node | ↑ Up: LeetCode 解题笔记 | Next: 118. Pascal’s Triangle →