友情支持
如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜
|
|
有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。
公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
62. 不同路径
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？
示例 1：
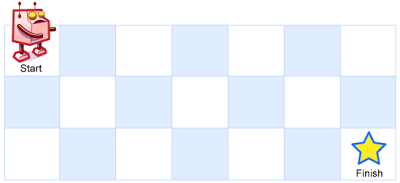
输入：m = 3, n = 7 输出：28
示例 2：
输入：m = 3, n = 2 输出：3 解释： 从左上角开始，总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
示例 3：
输入：m = 7, n = 3 输出：28
示例 4：
输入：m = 3, n = 3 输出：6
提示：
-
1 <= m, n <= 100 -
题目数据保证答案小于等于
2 * 109
思路分析
-
一刷
-
二刷
-
三刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2019-10-26 22:56
*/
public int uniquePaths(int m, int n) {
if (m == 0 || n == 0) {
return 0;
}
int[] row = new int[n];
Arrays.fill(row, 1);
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
row[j] = row[j - 1] + row[j];
}
}
return row[n - 1];
}
/**
* timeout
*/
public int uniquePathsBottomUp(int m, int n) {
if (m == 0 || n == 0) {
return 0;
}
if (m == 1 || n == 1) {
return 1;
}
return uniquePathsBottomUp(m - 1, n) + uniquePathsBottomUp(m, n - 1);
}
/**
* Runtime: 0 ms, faster than 100.00% of Java online submissions for Unique Paths.
* <p>
* Memory Usage: 33 MB, less than 5.10% of Java online submissions for Unique Paths.
*/
public int uniquePathsMatrix(int m, int n) {
if (m == 0 || n == 0) {
return 0;
}
int[][] paths = new int[m][n];
for (int i = 0; i < m; i++) {
paths[i][0] = 1;
}
for (int i = 1; i < n; i++) {
paths[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
paths[i][j] = paths[i - 1][j] + paths[i][j - 1];
}
}
return paths[m - 1][n - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2024-09-12 15:16:31
*/
public int uniquePaths(int m, int n) {
// 1. dp 表示走到某个节点一共有多少路径
int[][] dp = new int[m][n];
// 3. 第一行只有一种走法
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
// 3. 第一列也只有一种走法。
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
// 4. 遍历顺序：从左上逐步向右下遍历
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
// 2. 由于只能从上或者从左走过来，
// 那么路径数量就是两个节点相加
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-18 17:19:45
*/
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
dp[i][0] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}