友情支持
如果您觉得这个笔记对您有所帮助，看在D瓜哥码这么多字的辛苦上，请友情支持一下，D瓜哥感激不尽，😜
|
|
有些打赏的朋友希望可以加个好友，欢迎关注D 瓜哥的微信公众号，这样就可以通过公众号的回复直接给我发信息。
公众号的微信号是: jikerizhi。因为众所周知的原因，有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
116. Populating Next Right Pointers in Each Node
You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node left;
Node right;
Node *next;
}Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Follow up:
-
You may only use constant extra space.
-
Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.
Example 1:
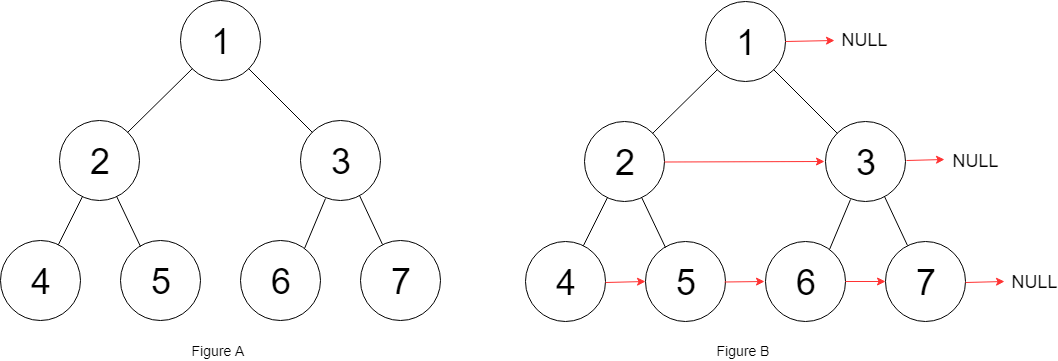
Input: root = [1,2,3,4,5,6,7] Output: [1,,2,3,,4,5,6,7,] Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '' signifying the end of each level.
Constraints:
-
The number of nodes in the given tree is less than
4096. -
-1000 ⇐ node.val ⇐ 1000
解题分析
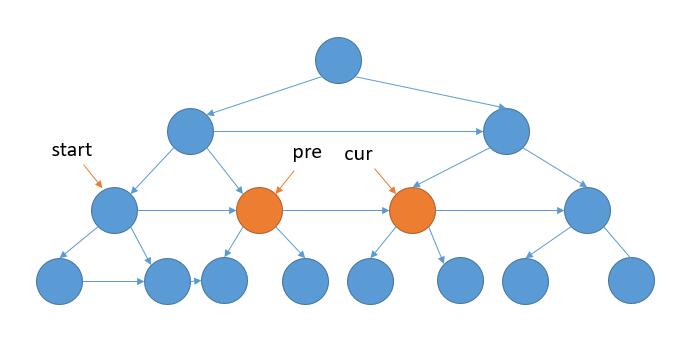
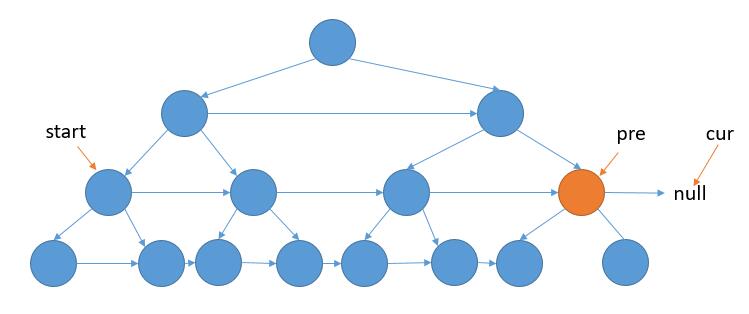
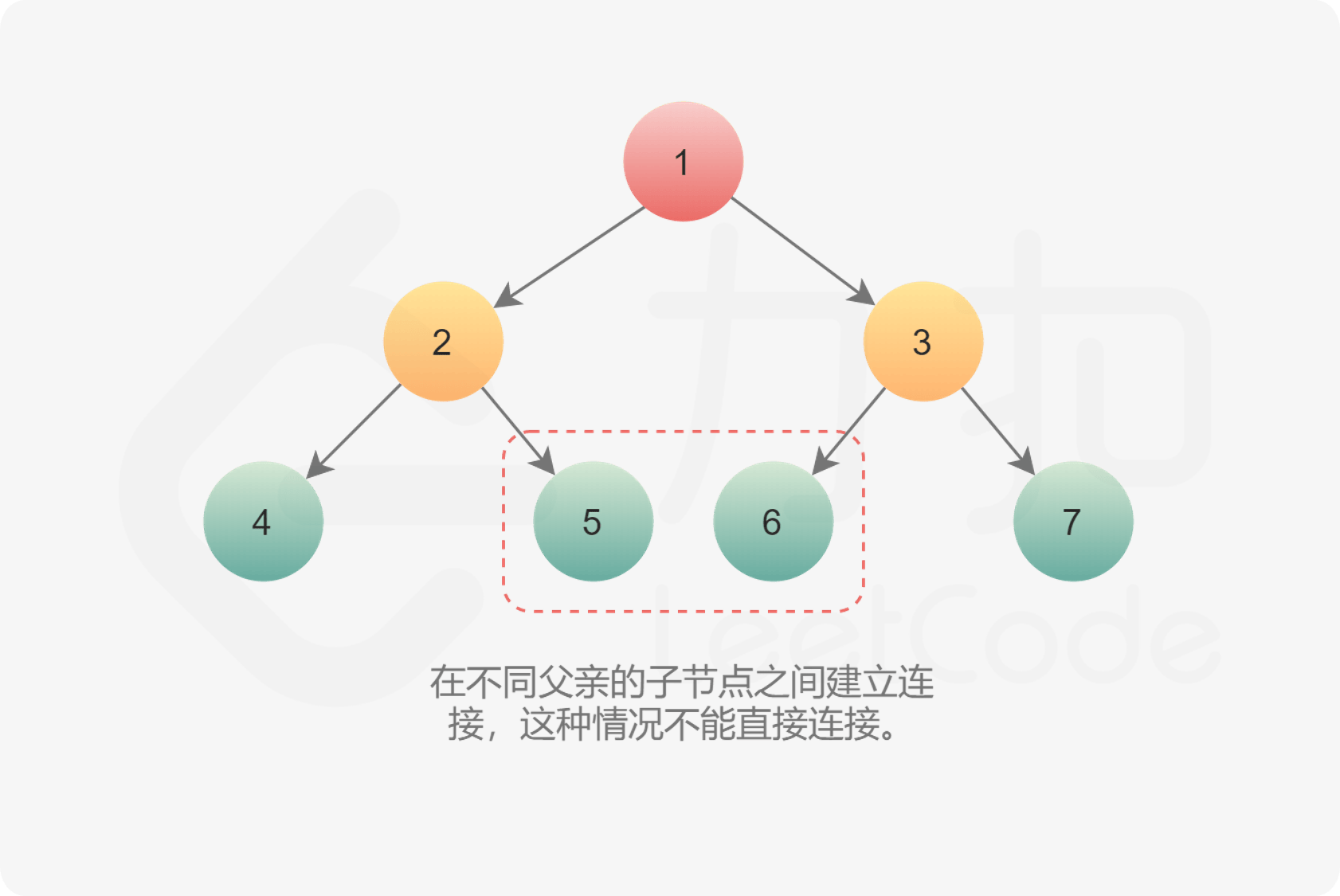
这道题的关键是在上层遍历中，把下层的链接关系建立起来。
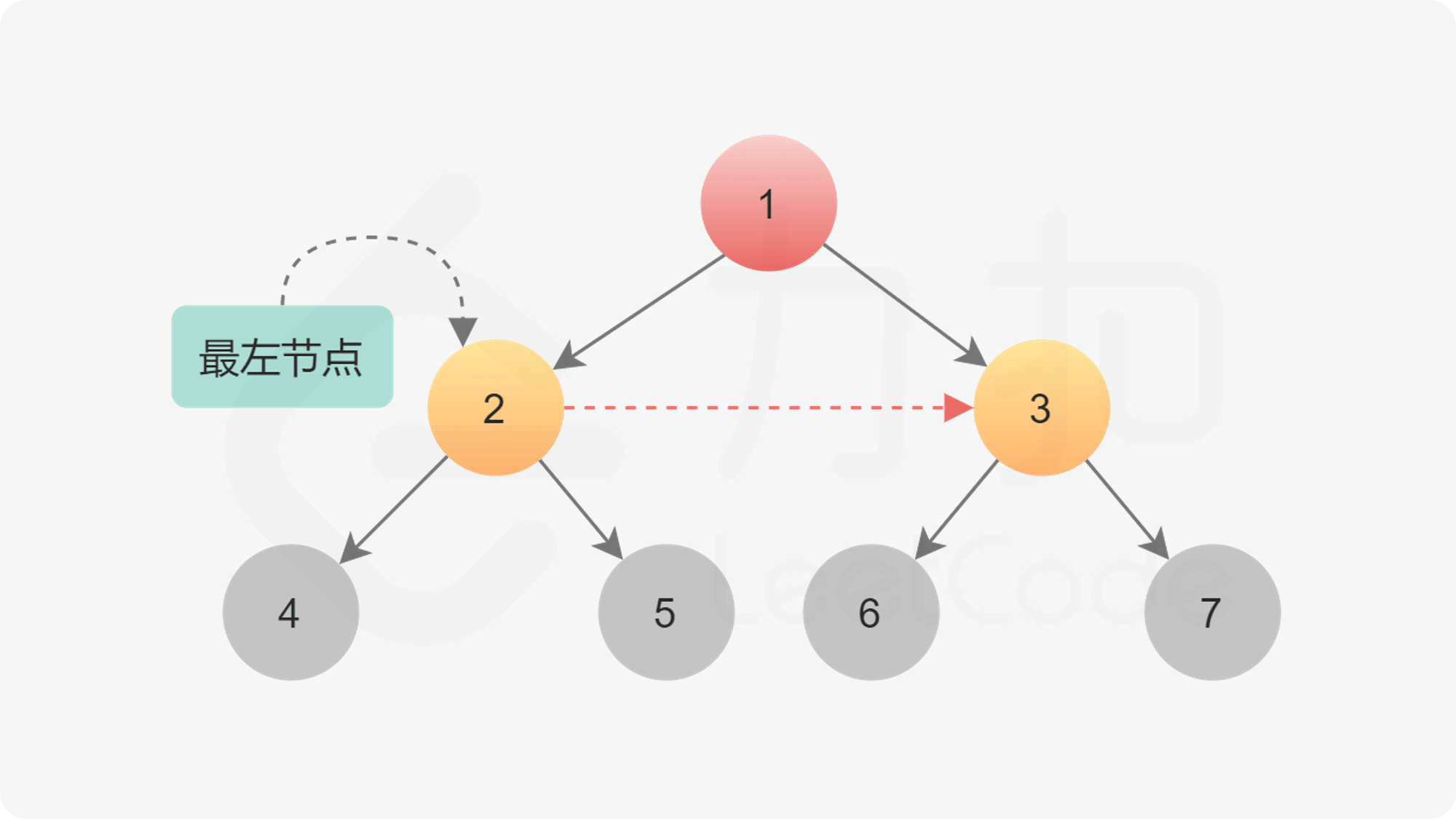
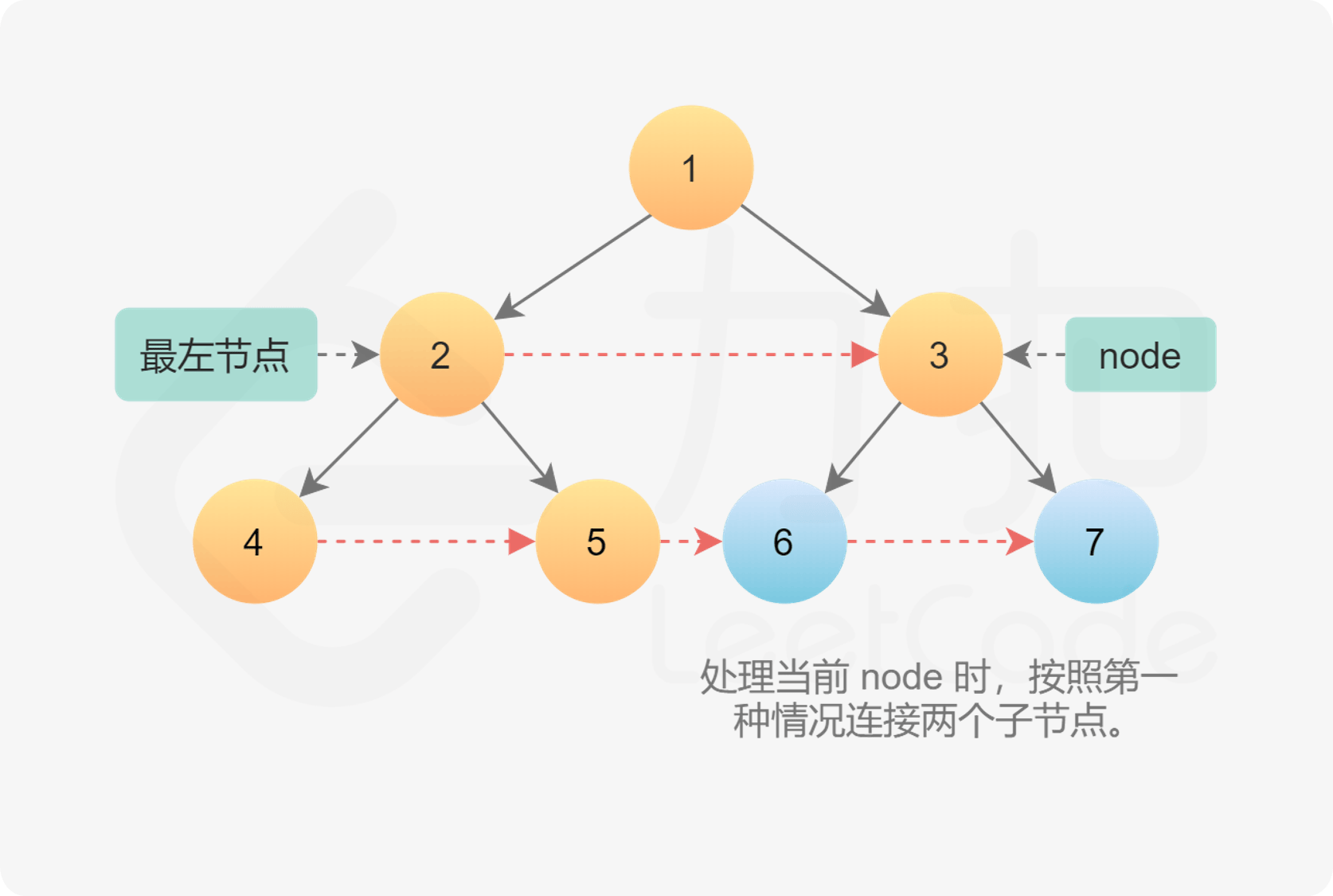
根据这个提示，再重新实现这个题目时，在思考的过程发现，最重要的就是保存每一层的最左节点。（这点也是根据树的 Morris 遍历得到的启发）这是每一层的起始位置。另外，每层循环的结束是当前节点为 null 了。（每层最后的一个节点没有 next 节点）。
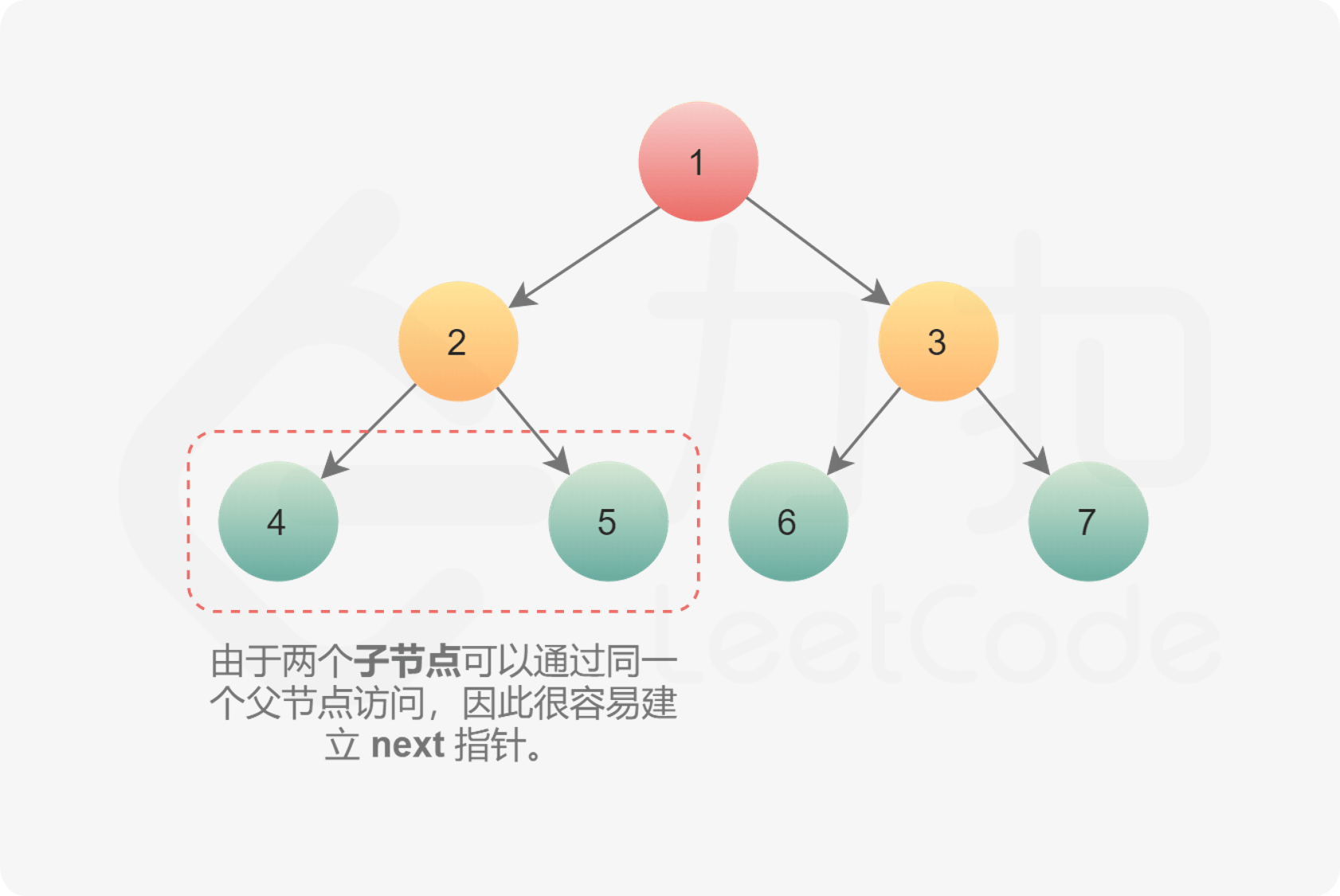
因为是完全二叉树。所以，如果左下节点为空则到达最后一层；向右节点为空，则到达行尾需要换行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
* Runtime: 1 ms, faster than 47.22% of Java online submissions for Populating Next Right Pointers in Each Node.
*
* Memory Usage: 48.3 MB, less than 6.35% of Java online submissions for Populating Next Right Pointers in Each Node.
*
* Copy from: https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by--27/[详细通俗的思路分析，多解法 - 填充每个节点的下一个右侧节点指针 - 力扣（LeetCode）]
*/
public Node connect(Node root) {
if (Objects.isNull(root)) {
return root;
}
Node start = root;
Node previous = root;
Node current = null;
while (Objects.nonNull(previous.left)) {
if (Objects.isNull(current)) {
previous.left.next = previous.right;
previous = start.left;
current = start.right;
start = previous;
} else {
previous.left.next = previous.right;
previous.right.next = current.left;
previous = previous.next;
current = current.next;
}
}
return root;
}
常规解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
* 按照层序遍历，从前向后建立链接即可。
*/
public Node connect(Node root) {
if (root == null) {
return null;
}
Queue<Node> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
Node pre = null;
for (int i = 0; i < size; i++) {
Node cur = queue.poll();
if (pre != null) {
pre.next = cur;
}
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
pre = cur;
}
}
return root;
}
常数空间复杂度解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
* 根据提示写出来的：在上一层建立下一层的链接。
*
* 根据思考的过程，最重要的就是保存每一层的最左节点。这是每一层的起始位置。
* 另外，每层循环的结束是当前节点为 `null` 了。（每层最后的一个节点没有 `next` 节点）。
*/
public Node connect(Node root) {
// 原始手写代码
// if (root == null) {
// return root;
// }
// Node mostLeft = root;
// while (mostLeft != null) {
// Node cur = mostLeft;
// mostLeft = mostLeft.left;
// // 这个变量不需要，因为可以通过 cur.next.left 获得
// Node right = null;
// while (cur != null) {
// if (right != null) {
// right.next = cur.left;
// }
// if (cur.left != null) {
// cur.left.next = cur.right;
// }
// right = cur.right;
// cur = cur.next;
// }
// }
// return root;
// 参考官方题解后的精简代码
if (root == null) {
return null;
}
// 重点有三个
// 1. 寻找最左节点
Node mostLeft = root;
while (mostLeft != null) {
// 遍历这一层节点组织成的链表，为下一层的节点更新 next 指针
Node cur = mostLeft;
// 3. 确定每层的结束条件
while (cur != null) {
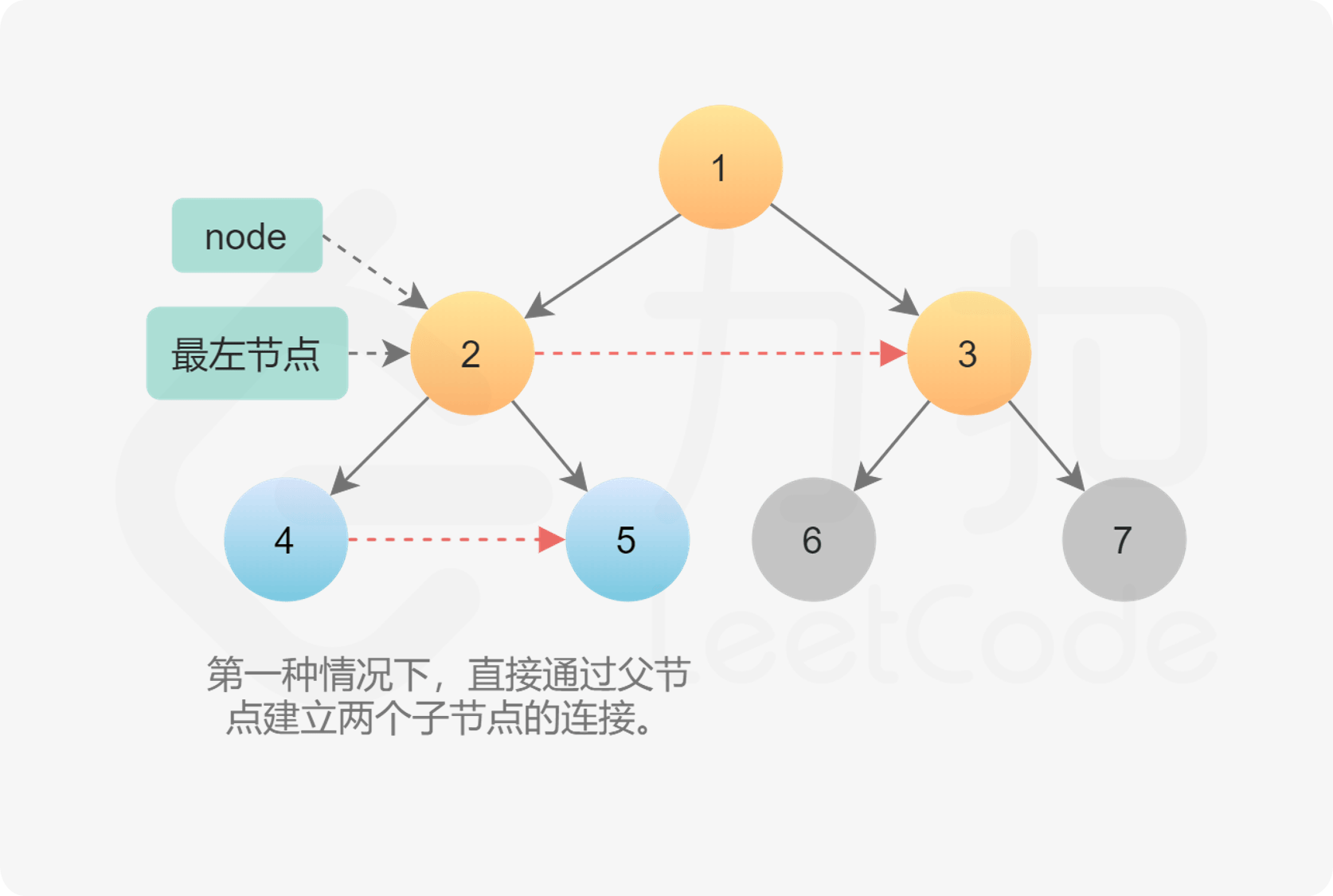
// 第一种情况：当前节点的左右子节点简历联系
if (cur.left != null) {
cur.left.next = cur.right;
}
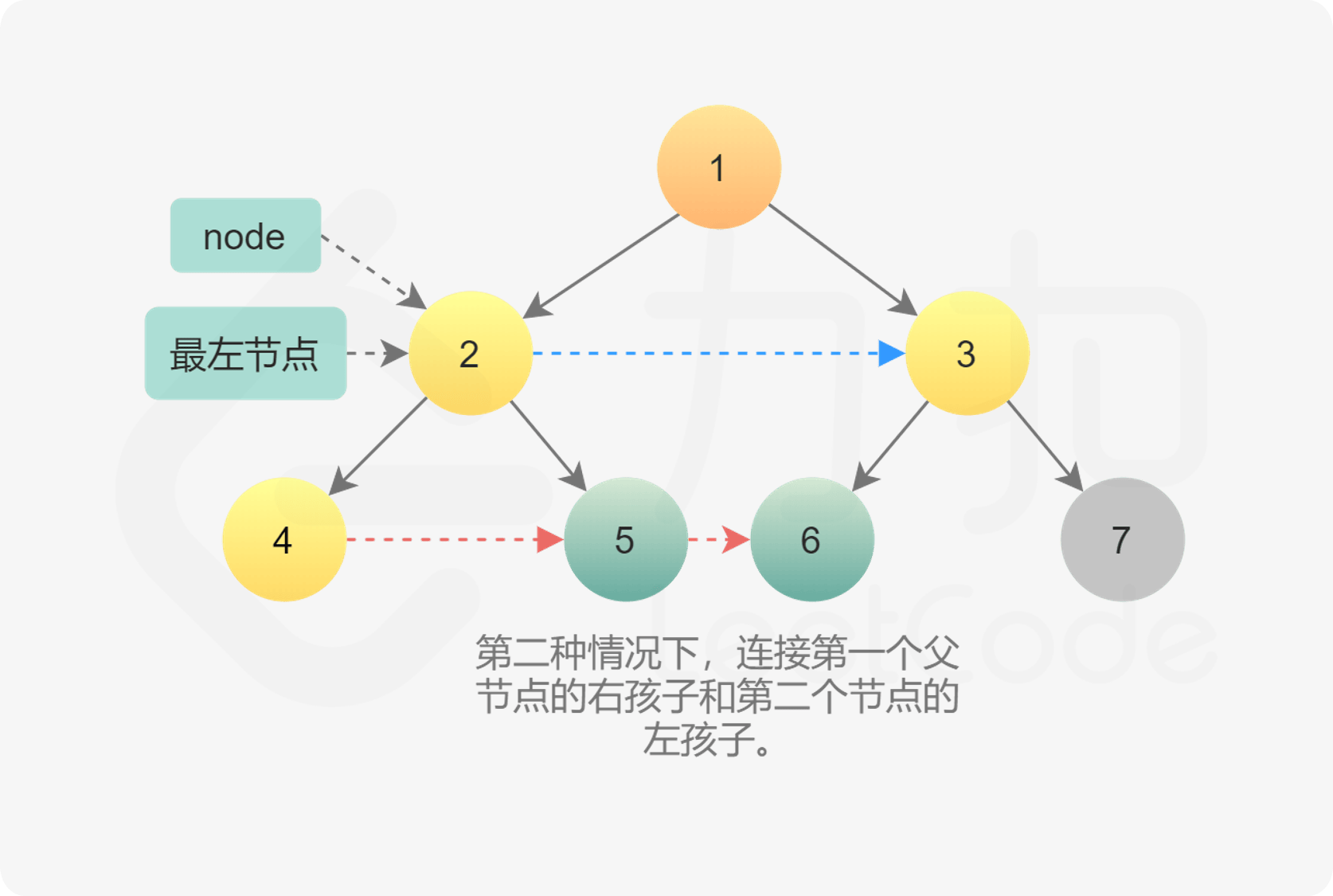
// 2. 建立左树右节点到右树左节点的链接
// 第二种情况：建立左树右节点到右树左节点的链接
if (cur.right != null && cur.next != null) {
cur.right.next = cur.next.left;
}
// 向后移动指针
cur = cur.next;
}
mostLeft = mostLeft.left;
}
return root;
}