友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
221. 最大正方形
在一个由 0 和 1 组成的二维矩阵内,找到只包含 1 的最大正方形,并返回其面积。
示例 1:
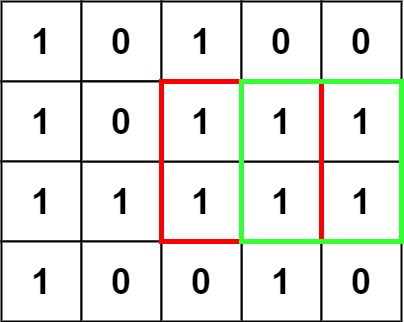
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出:4
示例 2:
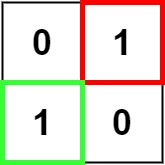
输入:matrix = [["0","1"],["1","0"]] 输出:1
示例 3:
输入:matrix = [["0"]] 输出:0
提示:
-
m == matrix.length -
n == matrix[i].length -
1 <= m, n <= 300 -
matrix[i][j]为0或1
思路分析
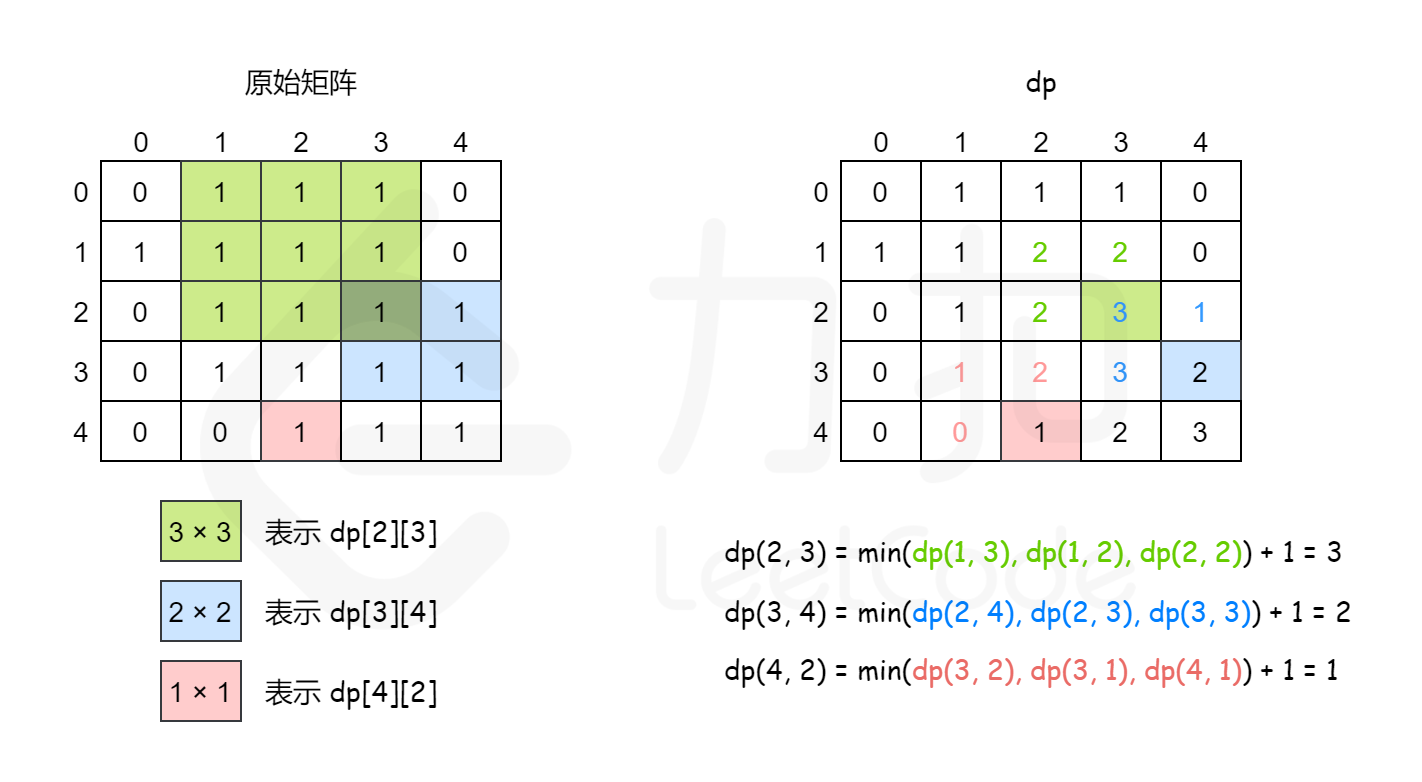
根据左上、左边、上边加自身,确定一个最小正方形;然后再进一步,在小正方形基础上,从四周选择已有正方形中最小,然后扩大,再这个过程中记录下最大的正方形边长,即可得到结果。思路如下图:
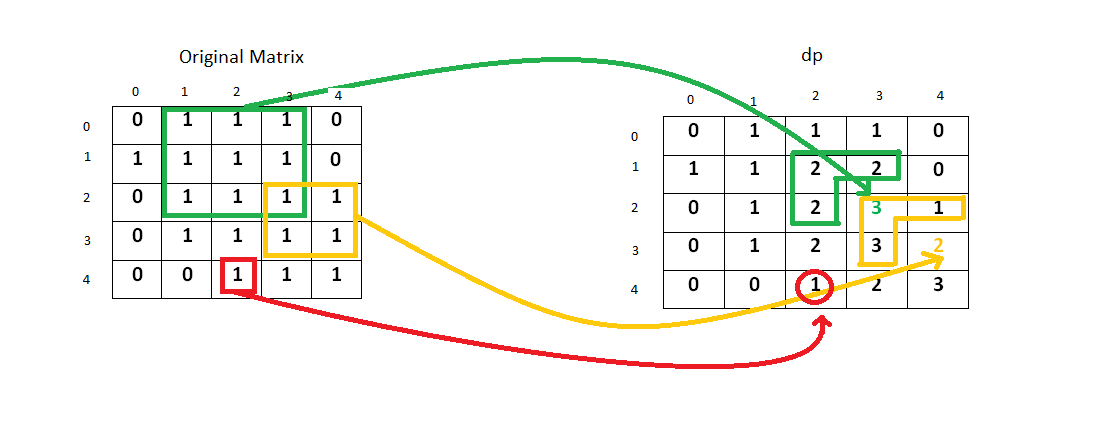
简化一下,不需要矩阵来存储所有正方形的计算结果,只需要一行来记录上一行计算结果和当前行计算结果即可。
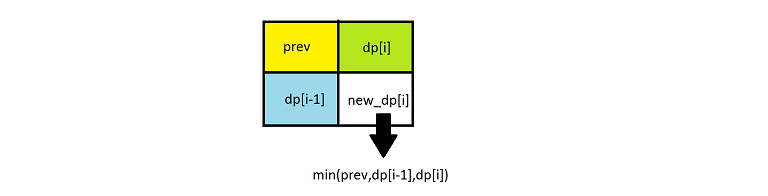
无需另外开辟矩阵存储中间结果,直接在参数矩阵上存储即可。
-
一刷
-
二刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/**
* Runtime: 4 ms, faster than 95.17% of Java online submissions for Maximal Square.
* Memory Usage: 43.3 MB, less than 91.18% of Java online submissions for Maximal Square.
*
* Copy from: https://leetcode.com/problems/maximal-square/solution/[Maximal Square solution - LeetCode]
*
* @author D瓜哥 · https://www.diguage.com
* @since 2020-01-28 12:21
*/
public int maximalSquare(char[][] matrix) {
if (Objects.isNull(matrix) || matrix.length == 0) {
return 0;
}
int yLength = matrix.length;
int xLength = matrix[0].length;
int[] dp = new int[xLength + 1];
int maxSideLength = 0;
int previous = 0;
for (int y = 1; y <= yLength; y++) {
for (int x = 1; x <= xLength; x++) {
int temp = dp[x];
if (matrix[y - 1][x - 1] == '1') {
dp[x] = Math.min(Math.min(previous, dp[x]), dp[x - 1]) + 1;
maxSideLength = Math.max(maxSideLength, dp[x]);
} else {
dp[x] = 0;
}
previous = temp;
}
}
return maxSideLength * maxSideLength;
}
/**
* Runtime: 13 ms, faster than 8.65% of Java online submissions for Maximal Square.
* Memory Usage: 43.9 MB, less than 64.71% of Java online submissions for Maximal Square.
*
* Copy from: https://leetcode.com/problems/maximal-square/solution/[Maximal Square solution - LeetCode]
*/
public int maximalSquareMatrix(char[][] matrix) {
if (Objects.isNull(matrix) || matrix.length == 0) {
return 0;
}
int yLength = matrix.length;
int xLength = matrix[0].length;
int[][] dp = new int[yLength + 1][xLength + 1];
int maxSideLength = 0;
for (int y = 1; y <= yLength; y++) {
for (int x = 1; x <= xLength; x++) {
if (matrix[y - 1][x - 1] == '1') {
dp[y][x] = Math.min(Math.min(dp[y - 1][x - 1], dp[y - 1][x]), dp[y][x - 1]) + 1;
maxSideLength = Math.max(maxSideLength, dp[y][x]);
}
}
}
return maxSideLength * maxSideLength;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-18 23:35:51
*/
public int maximalSquare(char[][] matrix) {
int row = matrix.length;
int col = matrix[0].length;
int result = 0;
for (int r = 0; r < row; r++) {
for (int c = 0; c < col; c++) {
if (matrix[r][c] == '0') {
continue;
}
// 加速
if (result == 0) {
result = 1;
}
char left = '0';
if (0 <= c - 1) {
left = matrix[r][c - 1];
}
// 加速
if (left == '0') {
continue;
}
char top = '0';
if (0 <= r - 1) {
top = matrix[r - 1][c];
}
// 加速
if (top == '0') {
continue;
}
char topLeft = matrix[r - 1][c - 1];
// 加速
if (topLeft == '0') {
continue;
}
matrix[r][c] = (char) (1 + Math.min(left, Math.min(topLeft, top)));
result = Math.max(result, matrix[r][c] - '0');
}
}
return result * result;
}

