友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
63. 不同路径 II
给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角(即 grid[0][0])。机器人尝试移动到 右下角(即 grid[m - 1][n - 1])。机器人每次只能向下或者向右移动一步。
网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。
返回机器人能够到达右下角的不同路径数量。
测试用例保证答案小于等于 2 * 109。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出:2 解释:3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径: 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]] 输出:1
提示:
-
m == obstacleGrid.length -
n == obstacleGrid[i].length -
1 <= m, n <= 100 -
obstacleGrid[i][j]为0或1
思路分析
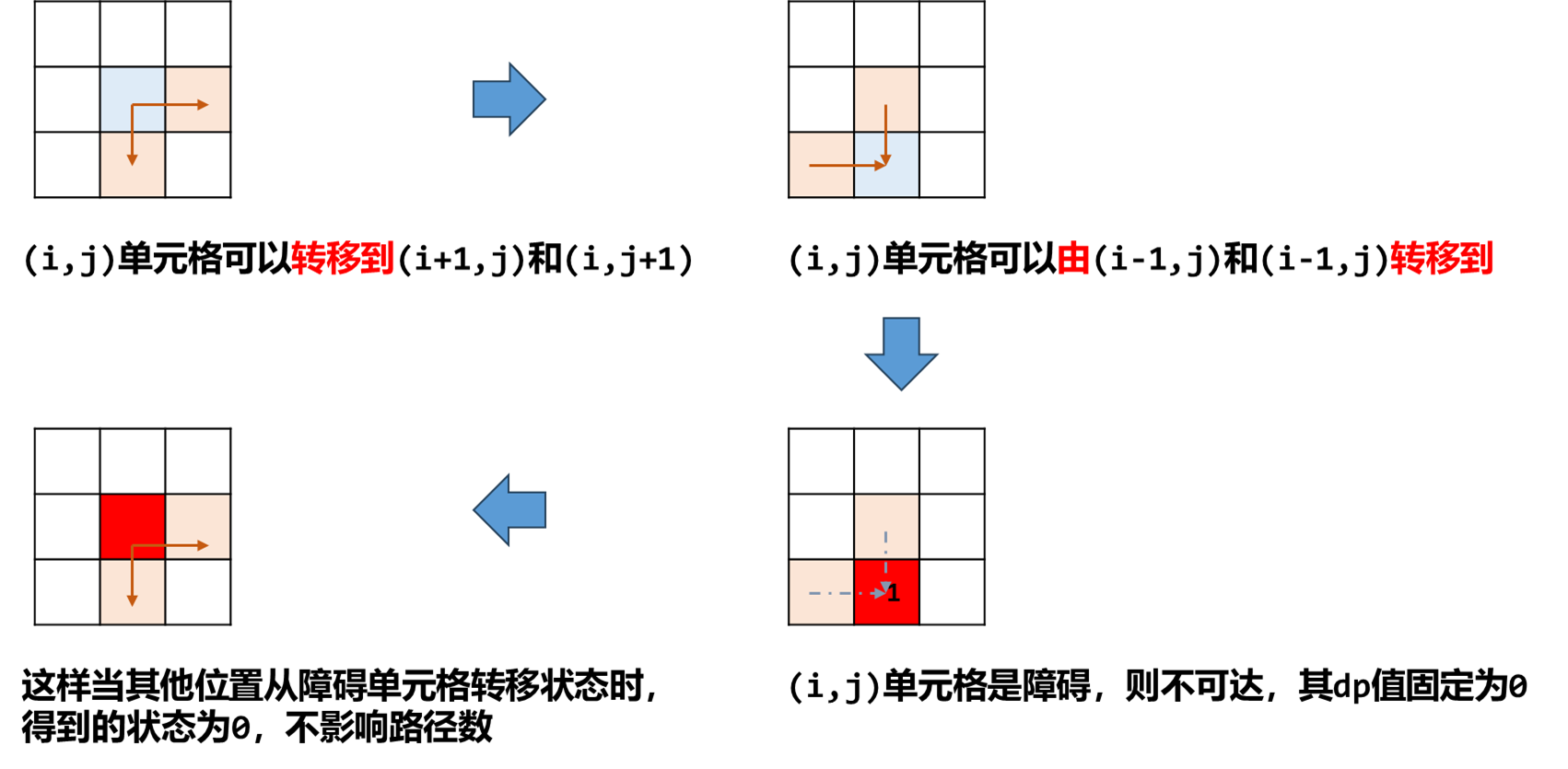
-
一刷
-
二刷
-
三刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
/**
* Runtime: 0 ms, faster than 100.00% of Java online submissions for Unique Paths II.
* <p>
* Memory Usage: 40.5 MB, less than 33.84% of Java online submissions for Unique Paths II.
*
* @author D瓜哥 · https://www.diguage.com
* @since 2019-10-26 23:50
*/
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if (Objects.isNull(obstacleGrid)
|| obstacleGrid.length == 0
|| obstacleGrid[0].length == 0
|| obstacleGrid[0][0] == 1) {
return 0;
}
obstacleGrid[0][0] = 1;
int m = obstacleGrid.length;
for (int i = 1; i < m; i++) {
if (obstacleGrid[i][0] == 0 && obstacleGrid[i - 1][0] == 1) {
obstacleGrid[i][0] = 1;
} else {
obstacleGrid[i][0] = 0;
}
}
int n = obstacleGrid[0].length;
for (int j = 1; j < n; j++) {
if (obstacleGrid[0][j] == 0 && obstacleGrid[0][j - 1] == 1) {
obstacleGrid[0][j] = 1;
} else {
obstacleGrid[0][j] = 0;
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) {
obstacleGrid[i][j] = 0;
} else {
obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1];
}
}
}
return obstacleGrid[m - 1][n - 1];
}
/**
* Runtime: 1 ms, faster than 23.04% of Java online submissions for Unique Paths II.
* <p>
* Memory Usage: 40.5 MB, less than 35.38% of Java online submissions for Unique Paths II.
*/
public int uniquePathsWithObstaclesMy(int[][] obstacleGrid) {
if (Objects.isNull(obstacleGrid)
|| obstacleGrid.length == 0
|| obstacleGrid[0].length == 0) {
return 0;
}
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
boolean hasObstacle = false;
for (int i = 0; i < n; i++) {
int value = obstacleGrid[0][i];
if (value == 1) {
hasObstacle = true;
obstacleGrid[0][i] = -1;
} else {
if (hasObstacle) {
obstacleGrid[0][i] = 0;
} else {
obstacleGrid[0][i] = 1;
}
}
}
hasObstacle = false;
if (obstacleGrid[0][0] == -1) {
hasObstacle = true;
}
for (int i = 1; i < m; i++) {
int value = obstacleGrid[i][0];
if (hasObstacle) {
obstacleGrid[i][0] = 0;
}
if (value == 1) {
hasObstacle = true;
obstacleGrid[i][0] = -1;
} else {
if (hasObstacle) {
obstacleGrid[i][0] = 0;
} else {
obstacleGrid[i][0] = 1;
}
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
int value = obstacleGrid[i][j];
if (value == 1) {
obstacleGrid[i][j] = -1;
} else {
int top = obstacleGrid[i - 1][j];
if (top == -1) {
top = 0;
}
int left = obstacleGrid[i][j - 1];
if (left == -1) {
left = 0;
}
obstacleGrid[i][j] = top + left;
}
}
}
return Math.max(obstacleGrid[m - 1][n - 1], 0);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2019-10-26 23:50
*/
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int row = obstacleGrid.length;
int column = obstacleGrid[0].length;
// 1. obstacleGrid 表示走到某个节点一共有多少路径
// 将障碍设置为-1,便于和 0 区分
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
if (obstacleGrid[i][j] == 1) {
obstacleGrid[i][j] = -1;
}
}
}
// 3. 第一行也只有一种走法,如果有障碍,则后面的路径为0
for (int i = 0; i < column; i++) {
if (obstacleGrid[0][i] == -1) {
break;
}
obstacleGrid[0][i] = 1;
}
// 3. 第一列只有一种走法,如果有障碍,则后面的路径为0
for (int i = 0; i < row; i++) {
if (obstacleGrid[i][0] == -1) {
break;
}
obstacleGrid[i][0] = 1;
}
printMatrix(obstacleGrid);
// 4. 确定遍历顺序:从左上向右下遍历
for (int i = 1; i < row; i++) {
for (int j = 1; j < column; j++) {
if (obstacleGrid[i][j] == -1) {
continue;
}
// 2. 确定递推公式
int mi = 0;
if (obstacleGrid[i - 1][j] != -1) {
mi = obstacleGrid[i - 1][j];
}
int ni = 0;
if (obstacleGrid[i][j - 1] != -1) {
ni = obstacleGrid[i][j - 1];
}
obstacleGrid[i][j] = mi + ni;
printMatrix(obstacleGrid);
}
}
return obstacleGrid[row - 1][column - 1] == -1 ? 0 : obstacleGrid[row - 1][column - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-04-18 17:32:04
*/
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
boolean obstacled = false;
boolean firstObstacle = obstacleGrid[0][0] == 1;
for (int i = 0; i < obstacleGrid[0].length; i++) {
if (obstacleGrid[0][i] == 1) {
obstacleGrid[0][i] = 0;
obstacled = true;
} else {
if (obstacled) {
obstacleGrid[0][i] = 0;
} else {
obstacleGrid[0][i] = 1;
}
}
}
obstacled = false;
int rows = obstacleGrid.length;
for (int i = 1; i < rows; i++) {
if (obstacleGrid[i][0] == 1) {
obstacleGrid[i][0] = 0;
obstacled = true;
} else {
if (obstacled || firstObstacle) {
obstacleGrid[i][0] = 0;
} else {
obstacleGrid[i][0] = 1;
}
}
}
for (int i = 1; i < rows; i++) {
for (int j = 1; j < obstacleGrid[i].length; j++) {
if (obstacleGrid[i][j] == 1) {
obstacleGrid[i][j] = 0;
} else {
obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1];
}
}
}
return obstacleGrid[rows - 1][obstacleGrid[rows - 1].length - 1];
}

