友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
909. 蛇梯棋
给你一个大小为 n x n 的整数矩阵 board ,方格按从 1 到 n2 编号,编号遵循
转行交替方式,从左下角开始 (即,从 board[n - 1][0] 开始)的每一行改变方向。
你一开始位于棋盘上的方格 1。每一回合,玩家需要从当前方格 curr 开始出发,按下述要求前进:
-
选定目标方格
next,目标方格的编号在范围[curr + 1, min(curr + 6, n2)]。-
该选择模拟了掷 六面体骰子 的情景,无论棋盘大小如何,玩家最多只能有 6 个目的地。
-
-
传送玩家:如果目标方格
next处存在蛇或梯子,那么玩家会传送到蛇或梯子的目的地。否则,玩家传送到目标方格next。 -
当玩家到达编号
n2的方格时,游戏结束。
如果 board[r][c] != -1 ,位于 r 行 c 列的棋盘格中可能存在 “蛇” 或 “梯子”。那个蛇或梯子的目的地将会是 board[r][c]。编号为 1 和 n2 的方格不是任何蛇或梯子的起点。
注意,玩家在每回合的前进过程中最多只能爬过蛇或梯子一次:就算目的地是另一条蛇或梯子的起点,玩家也 不能 继续移动。
-
举个例子,假设棋盘是
[[-1,4],[-1,3]],第一次移动,玩家的目标方格是2。那么这个玩家将会顺着梯子到达方格3,但 不能 顺着方格3上的梯子前往方格4。(简单来说,类似飞行棋,玩家掷出骰子点数后移动对应格数,遇到单向的路径(即梯子或蛇)可以直接跳到路径的终点,但如果多个路径首尾相连,也不能连续跳多个路径)
返回达到编号为 n2 的方格所需的最少移动次数,如果不可能,则返回 -1。
示例 1:
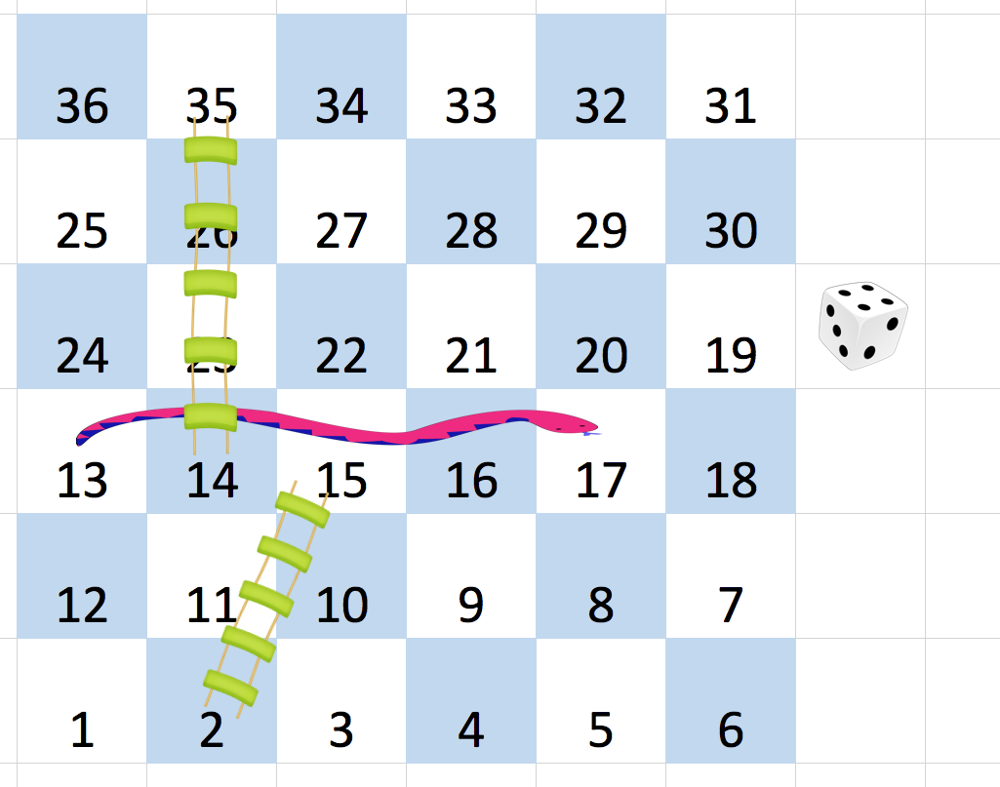
输入:board = [
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]
]
输出:4
解释:
首先,从方格 1 [第 5 行,第 0 列] 开始。
先决定移动到方格 2 ,并必须爬过梯子移动到到方格 15 。
然后决定移动到方格 17 [第 3 行,第 4 列],必须爬过蛇到方格 13 。
接着决定移动到方格 14 ,且必须通过梯子移动到方格 35 。
最后决定移动到方格 36 , 游戏结束。
可以证明需要至少 4 次移动才能到达最后一个方格,所以答案是 4 。
示例 2:
输入:board = [
[-1,-1],
[-1,3]
]
输出:1
提示:
-
n == board.length == board[i].length -
2 <= n <= 20 -
board[i][j]的值是-1或在范围[1, n2]内 -
编号为
1和n2的方格上没有蛇或梯子
思路分析
广度优先遍历!先建立矩阵坐标到数字和数字到矩阵坐标的关联关系!然后,就是出队,构建下一步到底的节点,再入队,直到终点,或者不可到达。
使用移位将坐标转换成一个数字,在一个 Map 对象中存正向和反向的对应关系。
看题解,可以把矩阵转换成一维数组,这样更高效,又学了一招!
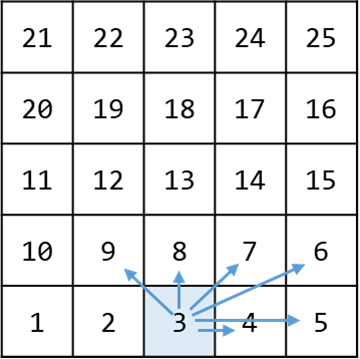
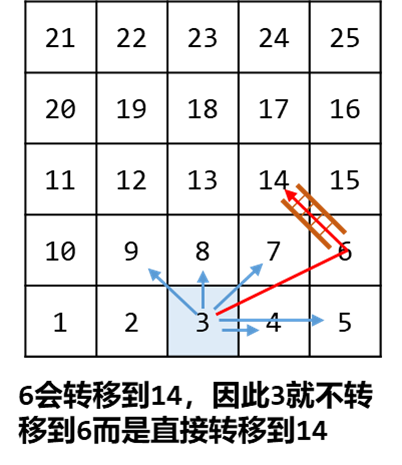
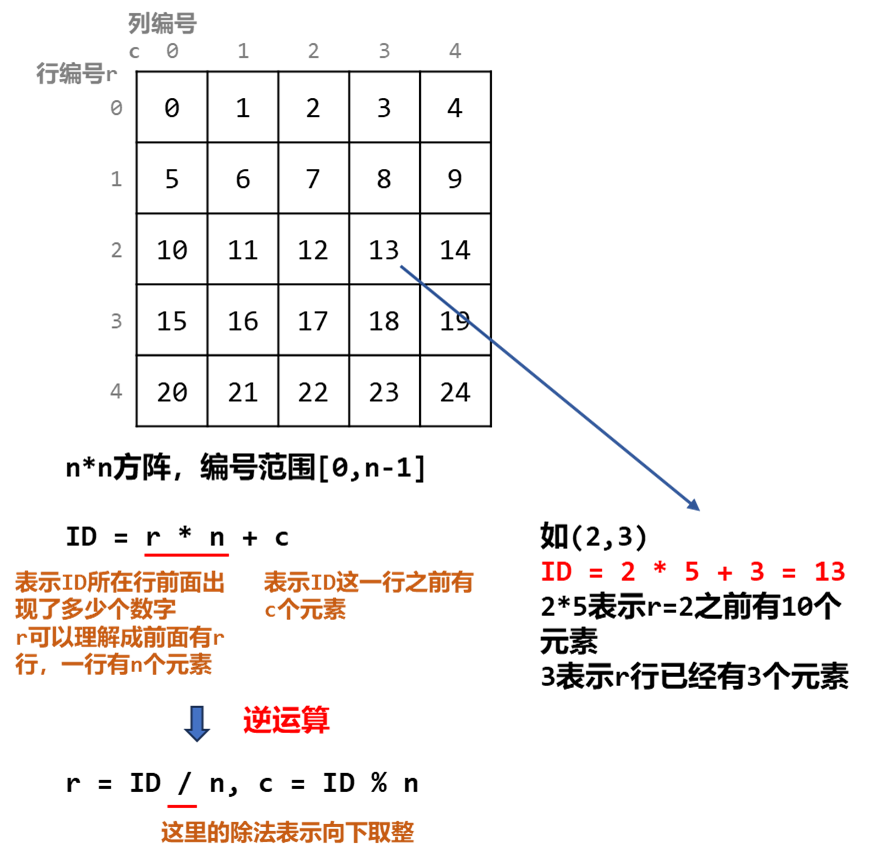
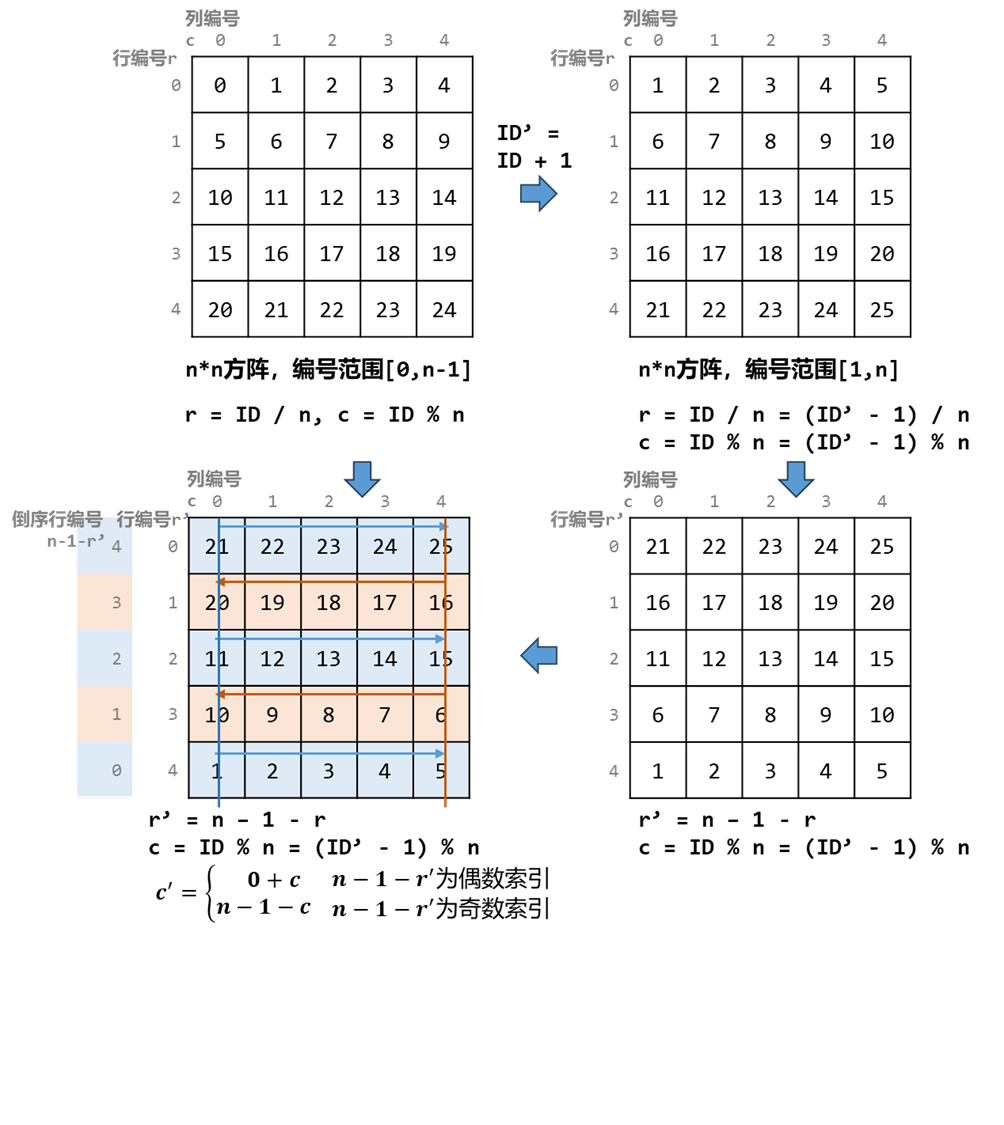
-
一刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-06-20 21:27:23
*/
public int snakesAndLadders(int[][] board) {
int n = board.length;
int max = n * n;
Map<Integer, Integer> matrix = buildMatrix(n);
Queue<Integer> queue = new LinkedList<>();
queue.offer(1);
int step = 0;
Set<Integer> visited = new HashSet<>();
while (!queue.isEmpty()) {
step++;
int size = queue.size();
Set<Integer> nextSteps = new HashSet<>();
for (int i = 0; i < size; i++) {
int cur = queue.poll();
visited.add(cur);
for (int j = 1; j <= 6; j++) {
int next = cur + j;
if (next >= max) {
return step;
}
// TODO 从 matrix 的使用情况来看,只需要构建数字到坐标的正向关联即可。
int[] point = decodeIndex(matrix.get(next));
int snake = board[point[0]][point[1]];
int nextStep = snake == -1 ? next : snake;
if (nextStep >= max) {
return step;
}
if (!visited.contains(nextStep)) {
nextSteps.add(nextStep);
}
}
}
queue.addAll(nextSteps);
}
return step;
}
private Map<Integer, Integer> buildMatrix(int n) {
Map<Integer, Integer> result = new HashMap<>();
for (int i = n - 1; i >= 0; i -= 2) {
for (int j = 0; j < n; j++) {
int num = (j + 1) + n * (n - i - 1);
int index = codeIndex(i, j);
result.put(num, index);
result.put(index, num);
}
if (i - 1 >= 0) {
for (int j = n - 1; j >= 0; j--) {
int num = 2 * n - j + n * (n - i - 1);
int index = codeIndex(i - 1, j);
result.put(num, index);
result.put(index, num);
}
}
}
return result;
}
private int[] decodeIndex(int index) {
int[] result = new int[2];
result[0] = index >> 18;
result[1] = (index >> 10) & 0xFF;
return result;
}
private int codeIndex(int i, int j) {
return (i << 18) + (j << 10);
}

