友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
427. 建立四叉树
给你一个 n * n 矩阵 grid ,矩阵由若干 0 和 1 组成。请你用四叉树表示该矩阵 grid 。
你需要返回能表示矩阵 grid 的 四叉树 的根结点。
四叉树数据结构中,每个内部节点只有四个子节点。此外,每个节点都有两个属性:
-
val:储存叶子结点所代表的区域的值。1 对应 True,0 对应 False。注意,当isLeaf为 False 时,你可以把 True 或者 False 赋值给节点,两种值都会被判题机制 接受 。 -
isLeaf: 当这个节点是一个叶子结点时为 True,如果它有 4 个子节点则为 False 。
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
我们可以按以下步骤为二维区域构建四叉树:
-
如果当前网格的值相同(即,全为
0或者全为1),将isLeaf设为 True ,将val设为网格相应的值,并将四个子节点都设为 Null 然后停止。 -
如果当前网格的值不同,将
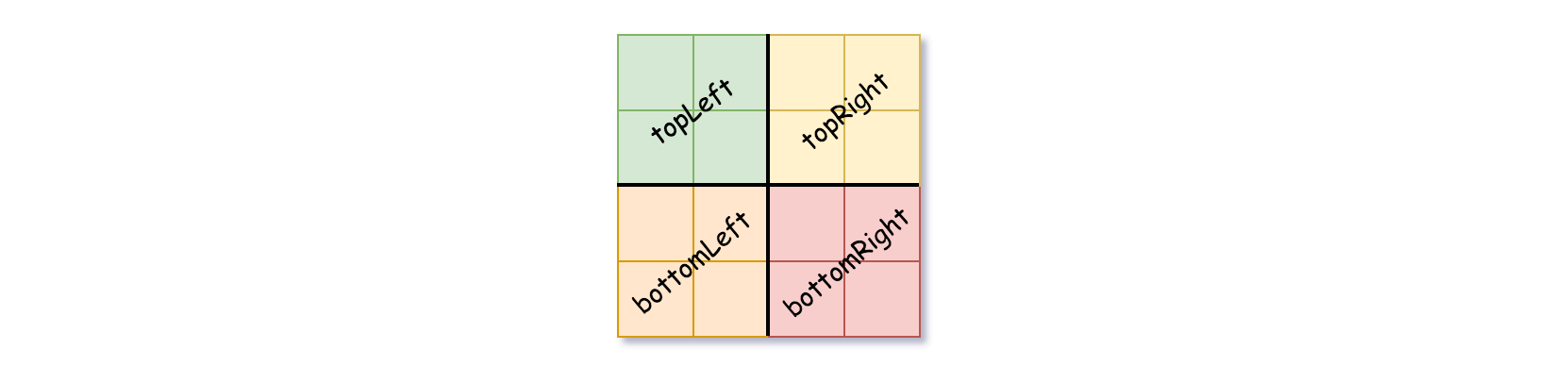
isLeaf设为 False, 将val设为任意值,然后如下图所示,将当前网格划分为四个子网格。 -
使用适当的子网格递归每个子节点。
如果你想了解更多关于四叉树的内容,可以参考 wiki 。
四叉树格式:
你不需要阅读本节来解决这个问题。只有当你想了解输出格式时才会这样做。输出为使用层序遍历后四叉树的序列化形式,其中 null 表示路径终止符,其下面不存在节点。
它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val]。
如果 isLeaf 或者 val 的值为 True,则表示它在列表 [isLeaf, val] 中的值为 1 ;如果 isLeaf 或者 val 的值为 False ,则表示值为 0 。
示例 1:

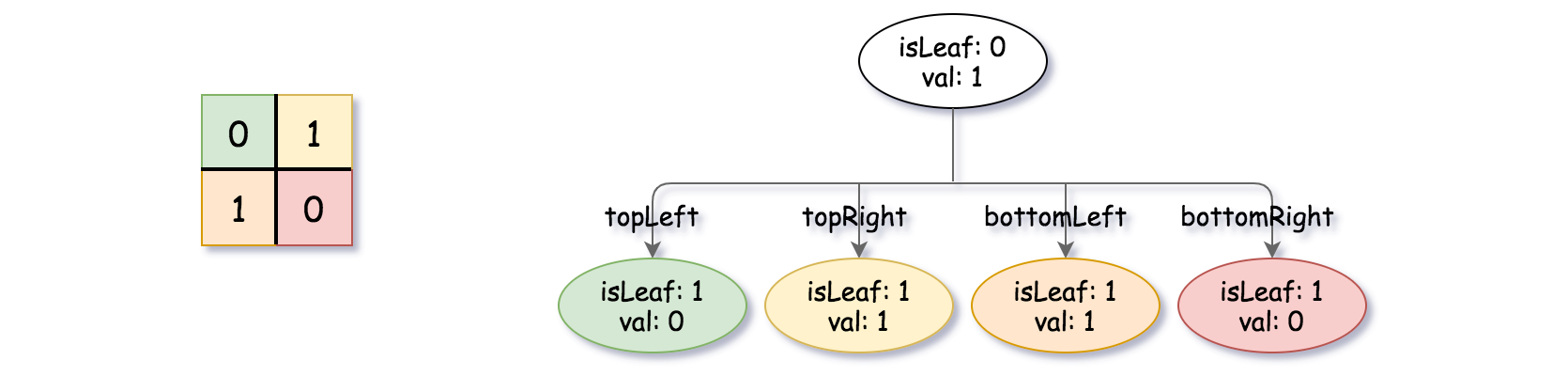
输入:grid = [[0,1],[1,0]] 输出:[[0,1],[1,0],[1,1],[1,1],[1,0]] 解释:此示例的解释如下: 请注意,在下面四叉树的图示中,0 表示 false,1 表示 True 。
示例 2:
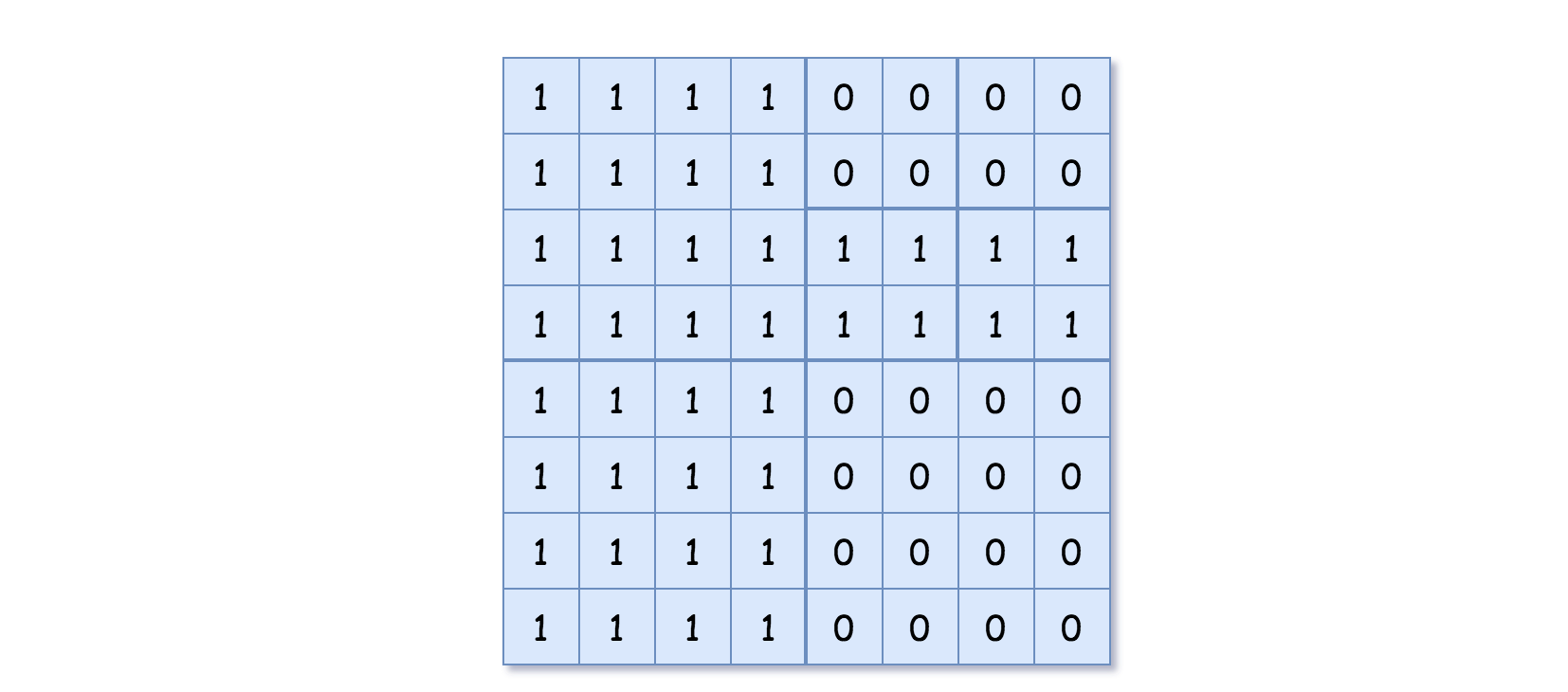
输入:grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]] 输出:[[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]] 解释:网格中的所有值都不相同。我们将网格划分为四个子网格。 topLeft,bottomLeft 和 bottomRight 均具有相同的值。 topRight 具有不同的值,因此我们将其再分为 4 个子网格,这样每个子网格都具有相同的值。 解释如下图所示:
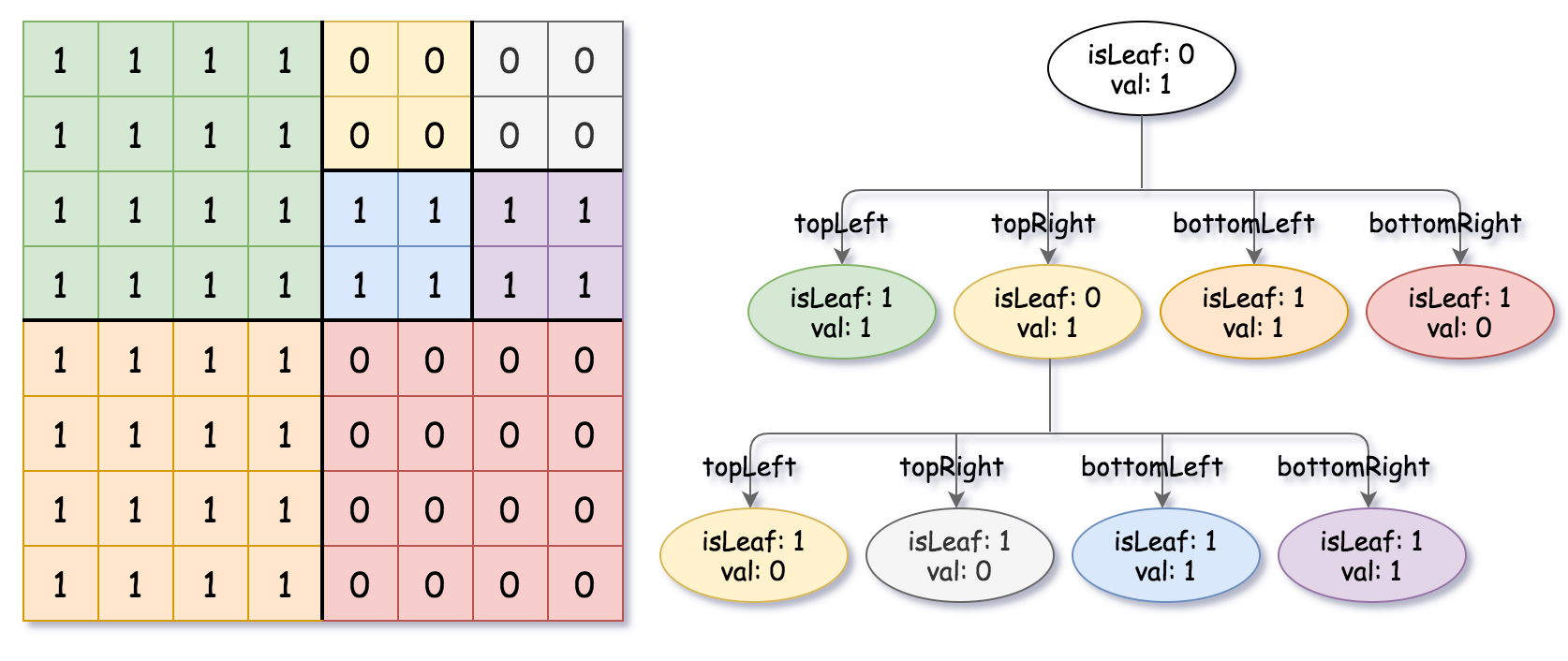
提示:
-
n == grid.length == grid[i].length -
n == 2x其中0 <= x <= 6
思路分析
递归+分治!
注意:一个区域内是否相等不能靠底层的节点来判断,需要遍历所有的节点值。
-
一刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-06-17 22:36:27
*/
public Node construct(int[][] grid) {
return dfs(grid, 0, 0, grid.length);
}
private Node dfs(int[][] grid, int row, int column, int length) {
if (length == 1) {
return new Node(grid[row][column] == 1, true);
}
boolean same = true;
for (int r = 0; r < length; r++) {
for (int c = 0; c < length; c++) {
if (grid[row][column] != grid[row + r][column + c]) {
same = false;
break;
}
}
if (!same) {
break;
}
}
if (same) {
return new Node(grid[row][column] == 1, true);
}
int nextLength = length / 2;
Node topLeft = dfs(grid, row, column, nextLength);
Node topRight = dfs(grid, row, column + nextLength, nextLength);
Node bottomLeft = dfs(grid, row + nextLength, column, nextLength);
Node bottomRight = dfs(grid, row + nextLength, column + nextLength, nextLength);
return new Node(true, false, topLeft, topRight, bottomLeft, bottomRight);
}

