友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
1006. 笨阶乘
通常,正整数 n 的阶乘是所有小于或等于 n 的正整数的乘积。例如,factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1。
相反,我们设计了一个笨阶乘 clumsy:在整数的递减序列中,我们以一个固定顺序的操作符序列来依次替换原有的乘法操作符:乘法(*),除法(/),加法(+)和减法(-)。
例如,clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1。然而,这些运算仍然使用通常的算术运算顺序:我们在任何加、减步骤之前执行所有的乘法和除法步骤,并且按从左到右处理乘法和除法步骤。
另外,我们使用的除法是地板除法(floor division),所以 10 * 9 / 8 等于 11。这保证结果是一个整数。
实现上面定义的笨函数:给定一个整数 N,它返回 N 的笨阶乘。
示例 1:
输入:4 输出:7 解释:7 = 4 * 3 / 2 + 1
示例 2:
输入:10 输出:12 解释:12 = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1
提示:
-
1 <= N <= 10000 -
-231 <= answer <= 231 - 1(答案保证符合 32 位整数。)
思路分析
看官方题解,可以把减法改成“加负数”,这样就可以极大地减少判断,可以直接按照“遇到乘除立即算,遇到加减先入栈”处理。
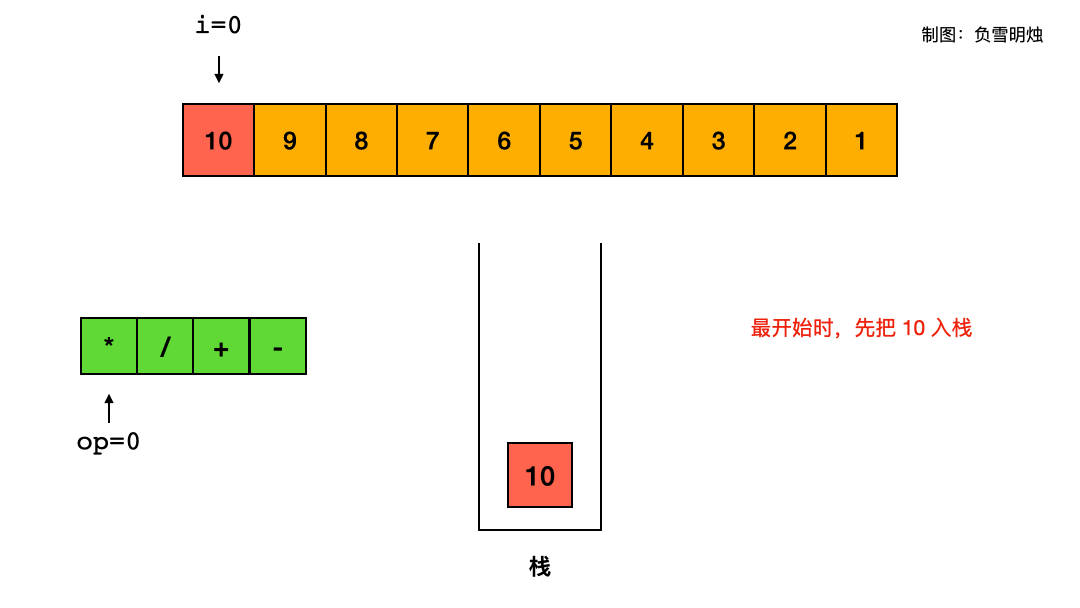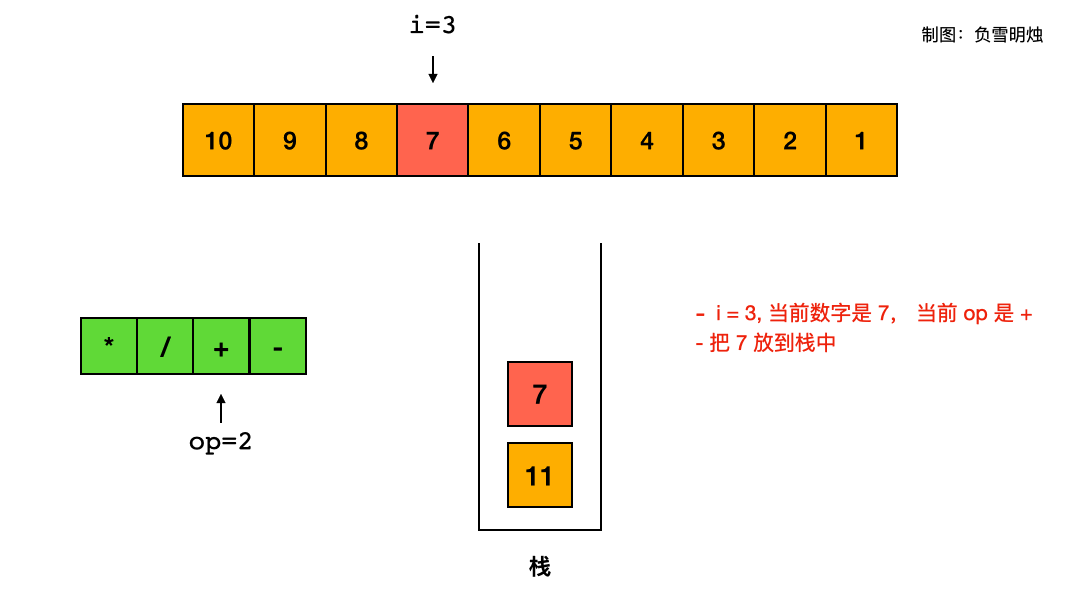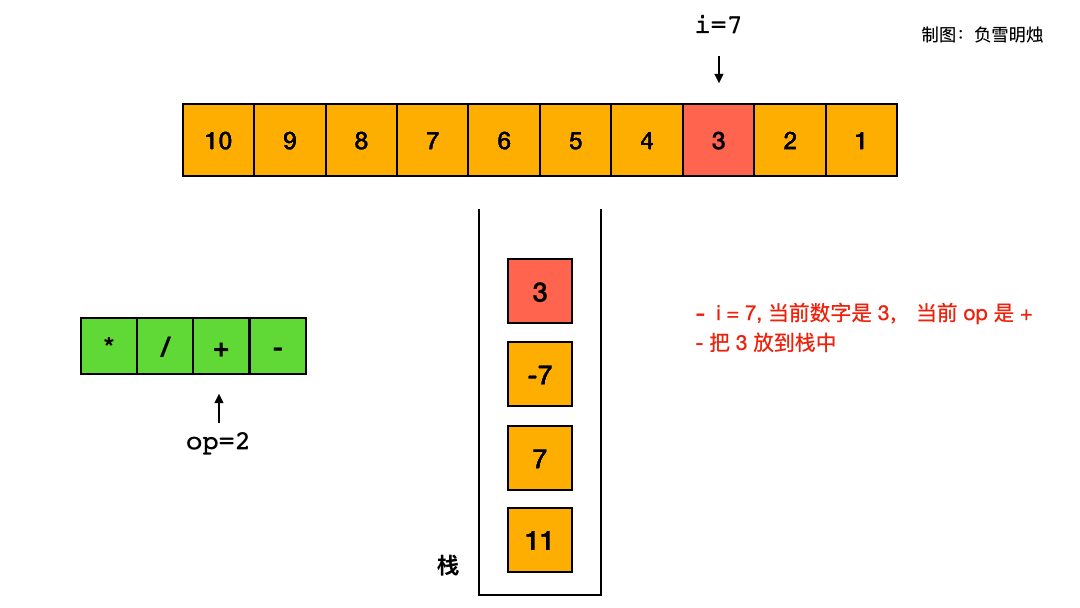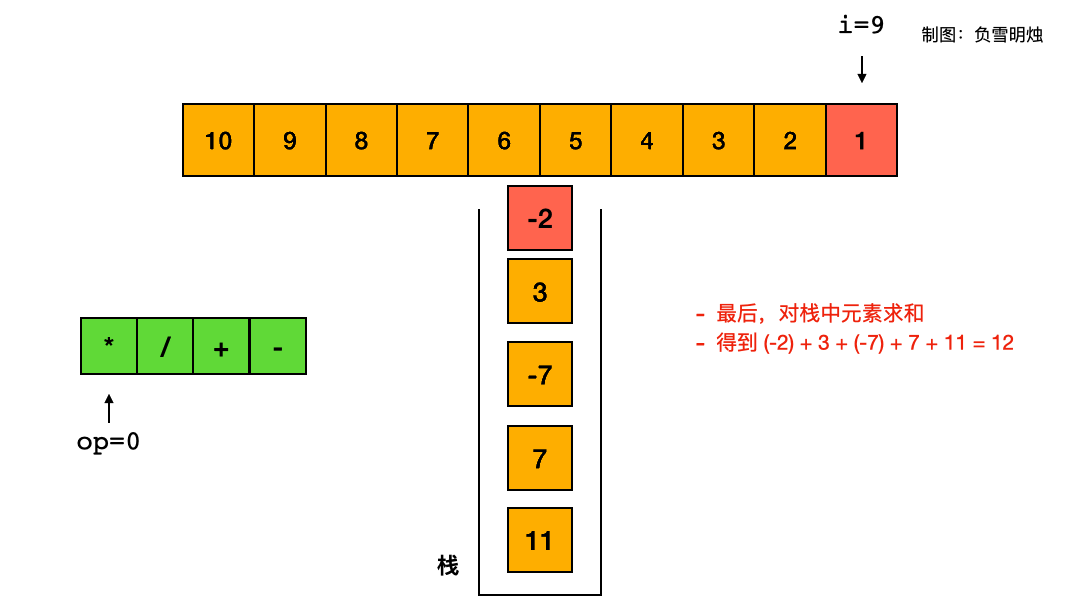
-
一刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-05-23 14:54:02
*/
public int clumsy(int n) {
char[] operators = new char[]{'*', '/', '+', '-'};
BiFunction<Integer, Integer, Integer>[] ops = new BiFunction[4];
ops[0] = (x, y) -> x * y;
ops[1] = (x, y) -> x / y;
ops[2] = Integer::sum;
ops[3] = (x, y) -> x - y;
int idx = 0;
int result = 0;
Deque<Integer> stack = new ArrayDeque<>(n);
stack.offer(n--);
while (!stack.isEmpty() && n > 0) {
if (idx == 2 && stack.size() == 2) {
Integer b = stack.pollLast();
Integer a = stack.pollLast();
stack.offer(ops[3].apply(a, b));
continue;
}
if (idx == 0 || idx == 1 || idx == 2) {
Integer pre = stack.pollLast();
Integer res = ops[idx].apply(pre, n--);
stack.offerLast(res);
} else {
stack.offerLast(n--);
}
idx++;
idx %= operators.length;
}
if (stack.size() == 1) {
result = stack.pollLast();
} else {
Integer b = stack.pollLast();
Integer a = stack.pollLast();
result = ops[3].apply(a, b);
}
return result;
}
参考资料
-
1006. 笨阶乘 - 官方题解 — 可以把减法改成“加负数”,这样就可以极大地减少判断。

