友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
457. 环形数组是否存在循环
存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数:
-
如果
nums[i]是正数,向前(下标递增方向)移动|nums[i]|步 -
如果
nums[i]是负数,向后(下标递减方向)移动|nums[i]|步
因为数组是 环形 的,所以可以假设从最后一个元素向前移动一步会到达第一个元素,而第一个元素向后移动一步会到达最后一个元素。
数组中的 循环 由长度为 k 的下标序列 seq 标识:
-
遵循上述移动规则将导致一组重复下标序列
seq[0] → seq[1] → … → seq[k - 1] → seq[0] → … -
所有
nums[seq[j]]应当不是 全正 就是 全负 -
k > 1
如果 nums 中存在循环,返回 true ;否则,返回 false 。
示例 1:
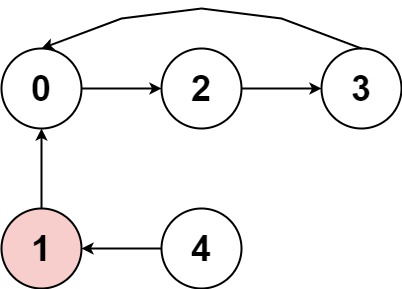
输入:nums = [2,-1,1,2,2] 输出:true 解释:图片展示了节点间如何连接。白色节点向前跳跃,而红色节点向后跳跃。 我们可以看到存在循环,按下标 0 -> 2 -> 3 -> 0 --> ...,并且其中的所有节点都是白色(以相同方向跳跃)。
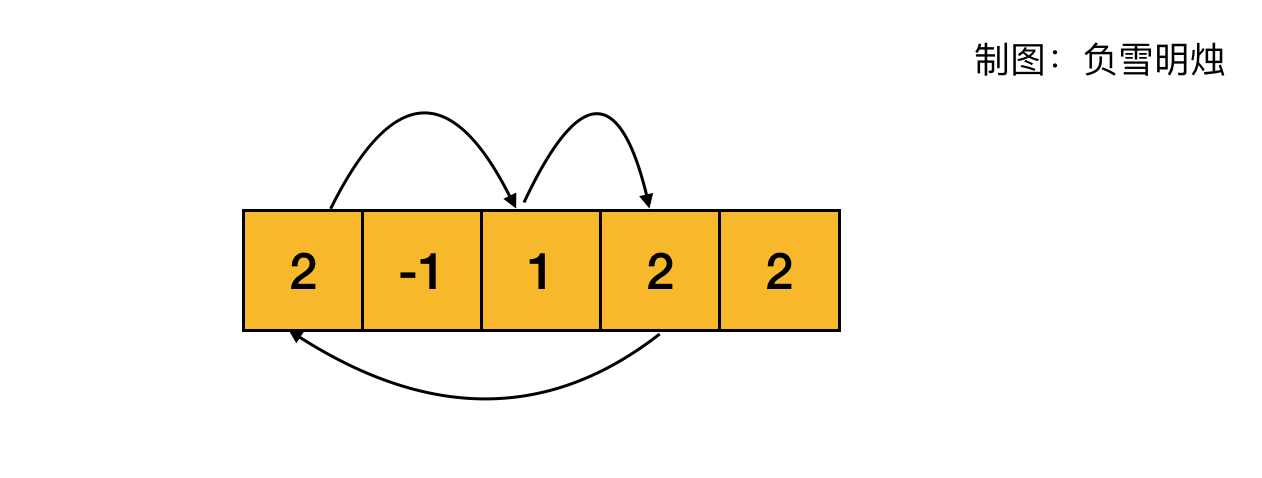
| 这个图更容易理解! |
示例 2:
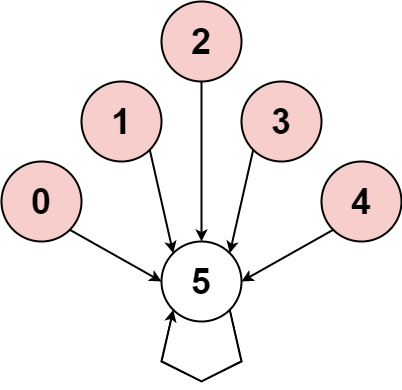
输入:nums = [-1,-2,-3,-4,-5,6] 输出:false 解释:图片展示了节点间如何连接。白色节点向前跳跃,而红色节点向后跳跃。 唯一的循环长度为 1,所以返回 false。
示例 3:
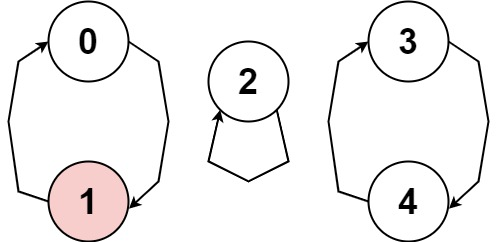
输入:nums = [1,-1,5,1,4] 输出:true 解释:图片展示了节点间如何连接。白色节点向前跳跃,而红色节点向后跳跃。 我们可以看到存在循环,按下标 0 --> 1 --> 0 --> ...,当它的大小大于 1 时,它有一个向前跳的节点和一个向后跳的节点,所以 它不是一个循环。 我们可以看到存在循环,按下标 3 --> 4 --> 3 --> ...,并且其中的所有节点都是白色(以相同方向跳跃)。
提示:
-
1 <= nums.length <= 5000 -
-1000 <= nums[i] <= 1000 -
nums[i] != 0
进阶:你能设计一个时间复杂度为 \(O(n)\) 且额外空间复杂度为 \(O(1)\) 的算法吗?
思路分析
使用回溯,对每一个坐标元素做深度优先遍历,发现环形数组则返回,否则继续向后遍历。时间复杂度是: \(O(n^2)\)。
进一步思考,遍历过的节点都不会是环形数组(是环形数组已经返回结果了),所以,可以把遍历过的节点留痕,那么遇到遍历过的节点,就可以直接返回 true 了。这样时间复杂度就成: \(O(n)\)。
另外,可以把遍历过的节点设置为 0,由于环形数组不能为 0,则遇到就可以直接“判断为 false”。
代码写的有些复杂了!
快慢指针也是一个非常好的思路:
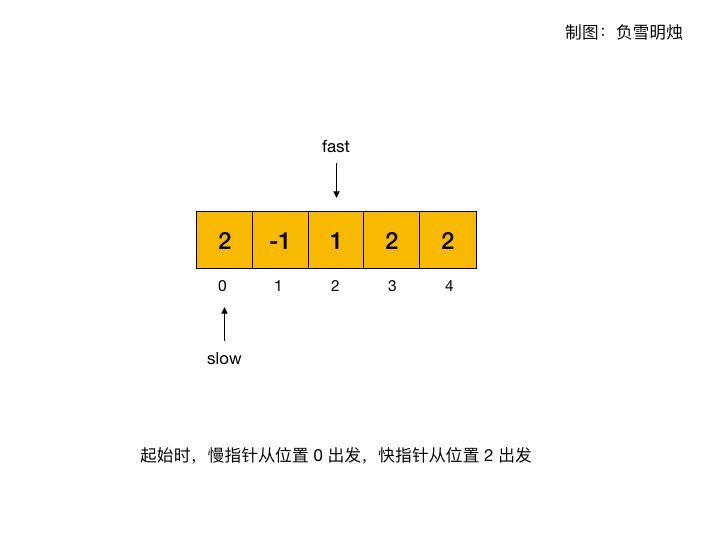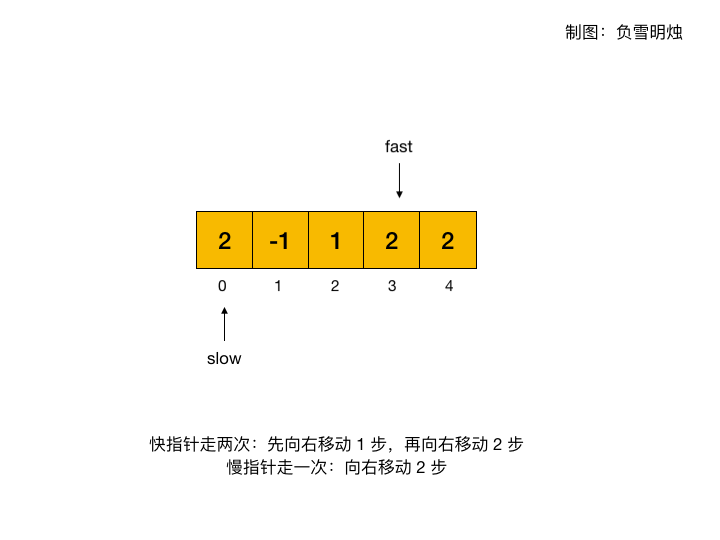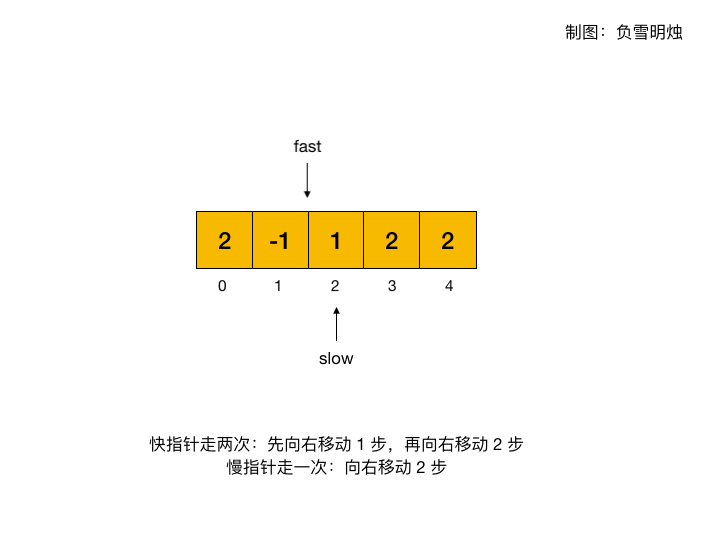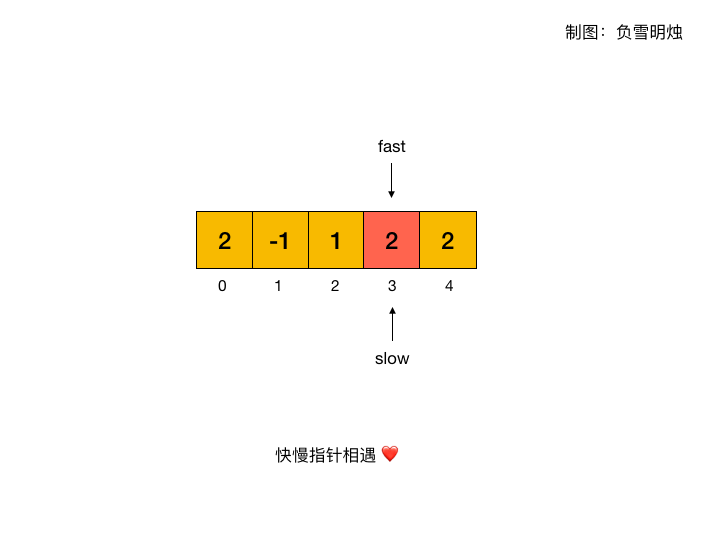
-
一刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
* 遍历过的节点都不会是环形数组(是环形数组已经返回结果了),
* 所以,可以把遍历过的节点留痕,那么遇到遍历过的节点,
* 就可以直接返回 true 了。这样时间复杂度就成了 O(n)。
*
* @author D瓜哥 · https://www.diguage.com
* @since 2025-08-23 21:19:58
*/
public boolean circularArrayLoop(int[] nums) {
int index = 2000 * nums.length;
int base = 100000;
for (int i = index; i < index + nums.length; i++) {
int num = nums[i % nums.length];
if (num < -1000) {
continue;
}
boolean circular = backtrack(nums, i, base, num > 0, 0, null);
if (circular) {
return true;
}
}
return false;
}
private boolean backtrack(int[] nums, int index, int base, boolean positive, int step, Integer last) {
int i = index % nums.length;
int num = nums[i];
if (num < -1000) {
return false;
} else if (positive ? num > base : 1000 < num && num < base) {
return step > 1 && last != null && !Objects.equals(last, i);
} else if ((num > 0) != positive) {
return false;
}
nums[i] = base + num;
boolean result = backtrack(nums, index + num, base, positive, step + 1, i);
nums[i] = -nums[i];
return result;
}

