友情支持
如果您觉得这个笔记对您有所帮助,看在D瓜哥码这么多字的辛苦上,请友情支持一下,D瓜哥感激不尽,😜
|
|
有些打赏的朋友希望可以加个好友,欢迎关注D 瓜哥的微信公众号,这样就可以通过公众号的回复直接给我发信息。

公众号的微信号是: jikerizhi。因为众所周知的原因,有时图片加载不出来。 如果图片加载不出来可以直接通过搜索微信号来查找我的公众号。 |
1557. 可以到达所有点的最少点数目
给你一个 有向无环图, n 个节点编号为 0 到 n-1 ,以及一个边数组 edges ,其中 edges[i] = [fromi, toi] 表示一条从点 `fromi 到点 `toi 的有向边。
找到最小的点集使得从这些点出发能到达图中所有点。题目保证解存在且唯一。
你可以以任意顺序返回这些节点编号。
示例 1:
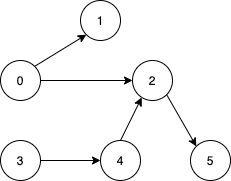
输入:n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]] 输出:[0,3] 解释:从单个节点出发无法到达所有节点。从 0 出发我们可以到达 [0,1,2,5] 。从 3 出发我们可以到达 [3,4,2,5] 。所以我们输出 [0,3] 。
示例 2:
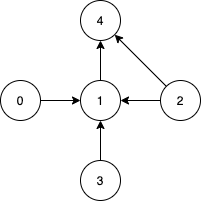
输入:n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]] 输出:[0,2,3] 解释:注意到节点 0,3 和 2 无法从其他节点到达,所以我们必须将它们包含在结果点集中,这些点都能到达节点 1 和 4 。
提示:
-
2 <= n <= 105 -
1 <= edges.length <= min(105, n * (n - 1) / 2) -
edges[i].length == 2 -
0 <= fromi, toi < n -
所有点对
(fromi, toi)互不相同。
思路分析
拓扑排序的基础款:利用拓扑排序的思路,构建“图”,寻找入度为 0 的节点即可。
看题解,发现一个更优解:不需要记录节点的入度,只需要标记有没有入度即可,没有入度就可以作为起点。所以,可以直接使用 boolean 类型的数组。空间利用率更高!
|
-
一刷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* @author D瓜哥 · https://www.diguage.com
* @since 2025-09-21 22:52:32
*/
public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
int[] inDegrees = new int[n];
for (List<Integer> edge : edges) {
Integer out = edge.getLast();
inDegrees[out]++;
}
List<Integer> result = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (inDegrees[i] == 0) {
result.add(i);
}
}
return result;
}

